|
|
| (67 intermediate revisions by 4 users not shown) |
| Line 1: |
Line 1: |
| {{Vorlage:TheorieTOC}} | | {{BlueM.Sim_nav}} |
| ==Natürliche und urbane Einzugsgebiete==
| | {{BlueMTheory_nav}} |
| __TOC__
| |
| Die Simulation natürlicher Einzugsgebiete verlangt die Bestimmung der Belastungsbildung, Abflussaufteilung und der Abflusskonzentration. Im Folgenden sind die zugrunde liegenden Berechnungsansätze aufgeführt.
| |
|
| |
|
| ===Belastungsbildung===
| | The natural process leading from rain to run-off is divided into three phases. The phases are Belastungsbildung, run-off generation (bzw. Belastungsaufteilung) and run-off concentration. The calculation approach for each of these phases is described in the following sections of this article. |
|
| |
|
| Die Belastungsbildung beschreibt die Ermittlung des Gebietsniederschlags für das betrachtete Einzugsgebiet. Pro Einzugsgebiet wird nur ein Niederschlag benutzt. Liegen mehrere Niederschlagsstationen im Einzugsgebiet vor, so ist es zweckmäßig das Gebiet in mehrere Systemelemente 'Einzugsgebiet' zu unterteilen, bis jedem Element wieder nur ein Niederschlag zugeordnet werden kann.
| |
|
| |
|
| ===Abflussbildung befestigter / unbefestigter Flächen=== | | ==Belastungsbildung== |
|
| |
|
| Die Abflussbildung ermittelt aus dem gefallenen Niederschlag den Effektivniederschlag und daraus abgeleitet die Komponenten Oberflächenabfluss, Infiltration, Verdunstung und Interflow. Eine Schneeberechnung wird durchgeführt bei Temperaturen unter Null °C und erfolgt anhand des Snow-Compaction-Verfahrens. Bezüglich der Algorithmen des Verfahrens wird auf die einschlägige Literatur verwiesen.
| |
|
| |
|
| Der natürlich ablaufende Prozess vom Niederschlag zum Abfluss wird für die mathematische Simulation in einzelne Phasen untergliedert. In der Abflussbildungsphase wird die Aufteilung des Niederschlages (Systembelastung) in den direkt zum Abfluss gelangenden "wirksamen Niederschlag" und die abflussunwirksamen Verluste (Benetzungs-, Mulden-, Verdunstungs-und Versickerungsverlust) vorgenommen. Dementsprechend wird diese Phase auch mit Belastungsaufteilung bezeichnet. Die resultierende mathematische Gleichung für die momentane Belastungsaufteilung schreibt sich wie folgt:
| | Die Belastungsbildung describes the determination of an areal rainfall for the considered catchment.Rainfall data is imported into BlueM via external time series. Therefore no explicit calculations are necessary for this phase. |
|
| |
|
| :<math>Nw(t) = N(t) - VP(t) - I(t) - \frac{dO}{dt} - \frac{dS}{dt}</math>
| |
|
| |
|
| :mit:
| | ==Run-off generation== |
| :NW = abflusswirksamer Niederschlag
| |
| :N = Niederschlag
| |
| :VP = potentielle Verdunstung
| |
| :I = Infiltration in den Bodenraum
| |
| :O = Oberflächenwasservorrat
| |
| :S = Schneevorrat
| |
|
| |
|
| Nachfolgend werden die in der Gleichung verwendeten Terme und deren Berechnung im Einzelnen erläutert.
| | In this phase surface run-off, infiltration, evaporation and interflow are determined by calculating the effective rainfall out of the fallen rain. Snow is calculated for temperatures below 0°C. The Snow-Compaction-Method {{:Literatur:Knauf_1980|Knauf}} is applied. |
|
| |
|
| ====Niederschlag N(t)====
| | Rainfall (system load) is divided into rainfall which directly generates run-off and run-off diminishing losses (wetting, trough, evaporation and infiltration losses). Therefore this phase is also called the Belastungsaufteilung. The mathematical equation for the momentary Belastungsaufteilung is as follows: |
|
| |
|
| Die Niederschlagsdaten müssen dem Simulationsmodell in Form von Regenreihen zur Verfügung gestellt werden. Hierbei ist es prinzipiell unerheblich, ob die Niederschlagsreihe ein Blockregen, ein Modellregen, ein gemessener natürlicher Regen, ein Regenspektrum oder eine langjährige Regenreihe ist. Je nach Zielsetzung der Simulationsrechnung ist die geeignete Belastung ausgewählt werden. Die Regenreihen stammen entweder aus der Zeitreihenverwaltung von TALSIM oder werden wie bei Anwendung einer Kurzfristprognose durch die Eingabe einer Regendauer, einer Niederschlagshöhe und der Wahl eines Modellregens direkt vor einer Simulation erzeugt.
| |
|
| |
|
| ====Verdunstung VP(t)==== | | :<math>Nw(t) = N(t) - VP(t) - I(t) - \frac{dO}{dt} - \frac{dS}{dt}</math> |
|
| |
|
| Die Verdunstung wirkt sich in zweifacher Weise auf die Abflussbildung aus. Zum einen sind die Anfangsbedingungen im Einzugsgebiet (Benetzung und Muldenfüllung auf der Oberfläche sowie eingeschränkt auch die Bodenfeuchte bei durchlässigen Flächen) ein Resultat des vor dem betrachteten Niederschlagsereignis stattfindenden Verdunstungsgeschehens, zum anderen wird der zu berechnende abflusswirksame Niederschlag um den Betrag der momentanen Verdunstungsrate geschmälert.
| | :mit: |
| | :NW = run-off generating rainfall |
| | :N = rainfall |
| | :VP = potential evaporation |
| | :I = infiltration into the soil |
| | :O = surfacce water reservoir content |
| | :S = snow reservoir content |
|
| |
|
| [[Bild:Theorie_Abb33.gif|thumb|Abbildung 33: Jahresgang der potentiellen Verdunstung nach BRANDT, 1979<ref name="brandt">'''Brandt, T.''' (1979): Modell zur Abflussgangliniensimulation unter Berücksichtigung des grundwasserbürtigen Abflusses, Technischer Bericht Nr. 24 aus dem Institut für Wasserbau, Fachgebiet Ingenieurhydrologie und Hydraulik der TH Darmstadt</ref>]]
| | The individual elements of the equation and the calculation of these elements is described in the following. |
|
| |
|
| Die potentielle (energetisch mögliche) Verdunstung VP ist zeitlich und örtlich sehr unterschiedlich und einer genauen Berechnung nur schwer zugänglich. Aus ausgewerteten Messungen von 20 Stationen, deren Mittelwerte als Histogramm in dargestellt sind, wurde folgende Ausgleichsfunktion (gepunktete Linie in [[:Bild:Theorie_Abb33.gif|Abbildung 33]]) ermittelt (BRANDT, 1979<ref name="brandt" />).
| |
|
| |
|
| :<math>VP[\mbox{mm}] = (0.96 + 0.0033 \cdot i) \cdot \sin(\frac{2 \pi}{365})(i - 148) + 1.58</math>
| | ===Rainfall N(t)=== |
|
| |
|
| :mit
| | BlueM requires rainfall data in form of rain time series. In general is does not matter if a block rain, Regenspektrum or a longtime rainfall time series. Depending on the purpose of the simulation the appropriate load (type) must be chosen. Rainfall time series originate out of the BlueM time series management <span class="TALSIM"> or are created immediately before simulation begin as is the case for short term prediction by supplying a rainfall duration, rainfall height and choosing a model rainfall </span>. |
| :i = laufender Tag des Abflussjahres
| |
| :i = 1 → 1. November
| |
|
| |
|
| [[Bild:Theorie_Abb34.gif|thumb|Abbildung 34: Tagesgang der potentiellen Verdunstung als Vielfaches der mittleren Tagesverdunstung]]
| |
|
| |
|
| Die jährliche potentielle Gesamtverdunstungshöhe beträgt 642 mm. Liegen keine gemessenen Verdunstungswerte vor, kann optional dieser normierte Jahresgang der potentiellen Verdunstung für die Berechnung der aktuellen Verdunstung herangezogen werden. Ist das gewählte Berechnungszeitintervall kleiner als ein Tag, wird mittels dem in [[:Bild:Theorie_Abb34.gif|Abbildung 34]] dargestellten Tagesgang letztendlich die potentielle Verdunstung für jedes Berechnungszeitintervall ermittelt. Ist das Berechnungsintervall ≥ 1 Tag entfällt die Berücksichtigung des Tagesganges.
| | ===Evaporation VP(t)=== |
| | There are two possibilities for the [[EZG-Datei|input]] of potential evaporation: |
|
| |
|
| ====Oberflächenwasservorrat (Versiegelter Flächenanteil) O==== | | ====a) annual evaporation ==== |
| | [[File:Theorie_Abb33.gif|thumb|Abbildung 33: annual pattern of potential evaporation according to {{:Literatur:Brandt_1979}}]] |
| | A normed annual pattern of potential evaporation according to {{:Literatur:Brandt_1979|Brandt}} is utilized for the calculation of potential evaporation. Through the evaluation of measurements from twenty different stations, whichs mean-values are depicted as a histogram in [[:File:Theorie_Abb33.gif|Abbildung 33]], the following smoothing function was derived (doted line in [[:File:Theorie_Abb33.gif|Abbildung 33]]): |
|
| |
|
| Bei den versiegelten Flächenanteilen kann neben dem Schneevorrat auch die Infiltration vernachlässigt werden, so dass sich die Bilanzgleichung wie folgt vereinfacht:
| | :<math>VP[\mbox{mm/d}] = \begin{cases}(0.96 + 0.0033 \cdot i) \cdot \sin(\frac{2 \pi}{365})(i - 148) + 1.58, & i <= 300 \\ 2.56 - 1.53 / 65. \cdot (i - 300.), & i > 300 \end{cases}</math> |
|
| |
|
| :<math>Nw(t) = N(t) - VP(t) - \frac{dO}{dt}</math> | | :´with |
| | :i = ongoing day of the hydrological year |
| | :i = 1 → 1. November |
|
| |
|
| wobei die Oberflächenwasservorratsänderung dO/dt die Benetzung der Oberfläche sowie die Auffüllung und Entleerung (durch Verdunstung) der Mulden repräsentiert.
| |
|
| |
|
| Als Benetzungsverlust BV für versiegelte Flächen wird folgender Standardwert angesetzt.
| | Potential evaporation according to Brandt refers to {{:Literatur:DVWK_1996|'''grass reference evaporation'''}} and assumes an annual total evaporation loss of 654,282 mm. If a different annual total evaporation loss is entered, the value determined by Brandt is scaled accordingly. |
|
| |
|
| :<code>BV = 0.5 mm</code>
| | ====b) evaporation time series==== |
| | If a evaporation time series is supplied the utilized time step is imported. <br/> |
| | ''Attention:'' For time steps < 1 day the time series value is additionally overprinted with a daily pattern! (Bug 1) |
|
| |
|
| Der Muldenverlust MV wird durch den Anwender vorgegeben. Der Standard- und gleichzeitig Maximalwert im Modell beträgt 1 mm.
| | ====daily pattern of evaporation==== |
| | [[File:Theorie_Abb34.gif|thumb|Abbildung 34: Daily pattern of potential evaporation as a multiple of mean daily evaporation]] |
| | If the chosen time step for the calculation is < 1 day the potential evaporation for each time step is calculated by taking the daily pattern depicted in [[:File:Theorie_Abb34.gif|Abbildung 34]] into consideration. If the chosen time step is ≥ 1 day the daily pattern is disregarded. |
|
| |
|
| Der Muldenverlust stellt den Mittelwert für eine geneigte Oberfläche dar. Da die Mulden jedoch nicht gleichmäßig verteilt sind und erfahrungsgemäß bereits ein Abfluss einsetzt, bevor überall die komplette Muldenauffüllung erreicht ist, wird unterstellt, dass jeweils
| |
|
| |
|
| [[Bild:Theorie_Abb35.gif|thumb|Abbildung 35: Schema der Modellansätze Benetzungs- und Muldenverluste]]
| | ===Surface water reservoir content(fraction of impervious area) O=== |
| | Snow reservoir content as well as infiltration can be neglected for impervious areas. Therefore the equation of balance is reduced to: |
|
| |
|
| * 1/3 der versiegelten Fläche einen verminderten Muldenverlust von 1/3 MV
| | :<math>Nw(t) = N(t) - VP(t) - \frac{dO}{dt}</math> |
| * 1/3 der versiegelten Fläche den mittleren Muldenverlust von 3/3 MV
| |
| * 1/3 der versiegelten Fläche einen erhöhten Muldenverlust von 5/3 MV
| |
|
| |
|
| aufweist. Somit kommt es bereits zum Abfluss, wenn der um die Verdunstungsrate verminderte Niederschlag den Benetzungsverlust und 1/3 des Muldenverlustes übersteigt (bei trockener Vorgeschichte). In [[:Bild:Theorie_Abb35.gif|Abbildung 35]] sind die o.g. Annahmen schematisch skizziert.
| | in which the change in surface water reservoir content <code>dO/dt</code> represents wetting of the surface as well as filling and depletion of water (through evaporation) in troughs. |
|
| |
|
| Der Abflussbeiwert der versiegelten Flächen (nach Abdeckung der Anfangsverluste) wird mit ψ = 1 angesetzt. Bei der Festlegung des versiegelten Flächenanteils in einem Teileinzugsgebiet ist zu beachten, dass nicht alle befestigten oder versiegelten Flächen tatsächlich in eine Kanalisation entwässern.
| | The wetting loss (BV) for impervious areas is set to the following standard value. |
|
| |
|
| Die kontinuierliche Bereitstellung der Benetzungs- und Muldenverluste erfolgt über die laufende Bilanzierung dieser Speicher und der Verdunstung.
| | :<code>BV = 0.5 mm</code> |
| | |
| ====Oberflächenwasservorrat (unversiegelter Flächenanteil) O====
| |
| | |
| Der Oberflächenwasservorrat wird über die Bilanzierung eines Verlustspeichers in Abhängigkeit des gewählten Abflussbildungsansatzes berechnet. Einzelheiten dazu finden sich in den folgenden Abschnitten zur Berechnung der Infiltration bzw. abflusswirksamer Niederschlag.
| |
| | |
| ====Infiltration bzw. abflusswirksamer Niederschlag I(t), Nw(t)====
| |
| | |
| Bei den durchlässigen Flächen kann die Infiltration in den Boden nicht vernachlässigt werden, da diese das Abflussgeschehen entscheidend prägt. Für die Berechnung wurden drei Ansätze im Modell implementiert:
| |
| | |
| # Konstanter Abflussbeiwert ψ
| |
| # Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)
| |
| # Bodenfeuchtesimulation
| |
| | |
| =====Konstanter Abflussbeiwert ψ=====
| |
| | |
| Bei Angabe eines ψ<sub>u</sub>-Wertes kommt nach Abdeckung der Anfangsverluste (Benetzungs- und Muldenverlust) der übrige Anteil des Niederschlages im Verhältnis des Abflussbeiwertes ψ<sub>u</sub> zum Abfluss und zwar unabhängig von der Vorgeschichte und den Merkmalen des Niederschlages (Höhe, Intensität, Dauer). Auf diesen Ansatz sollte nach Möglichkeit verzichtet werden, da hier der Prozess der Abflussbildung nur grob vereinfachend beschrieben wird.
| |
| | |
| =====Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)=====
| |
| | |
| Bei Angabe eines vom Bodentyp und der Bodennutzung abhängigen CN-Wertes (siehe DVWK, 1991<ref>'''DVWK''' (1991): Beitrag zur Bestimmung des effektiven Niederschlags für Bemessungshochwasser aus Gebietskenngrößen. Untersuchung des Fachausschusses "Niederschlag-Abfluß-Modelle", Materialien, Heft 2</ref>) lässt sich ein vorgeschichtsabhängiger Anfangsverlust sowie eine vorgeschichtsabhängige Beziehung des Abflussbeiwertes von der bis zum betrachteten Zeitpunkt akkumulierten Niederschlagshöhe formulieren (Zaiss, 1987<ref>'''Zaiß, H.''' (1989): Simulation ereignisspezifischer Einflüsse des Niederschlag-Abfluß-Prozesses von Hochwasserereignissen kleiner Einzugsgebiete mit N-A-Modellen. Technischer Bericht des Instituts für Ingenieurhydrologie und Hydraulik, TH Darmstadt, Nr. 42</ref>); d.h. der Abflussbeiwert wächst mit zunehmendem Niederschlag im Verlauf des Ereignisses an.
| |
| | |
| Die Quantifizierung der Vorgeschichte erfolgt über den 21-Tage-Vorregenindex VN
| |
| | |
| :<math>V_N = \sum_{j=1}^{21} C(j)^j \cdot h_{N,j}</math>
| |
| | |
| :mit
| |
| :h<sub>N,j</sub> = Niederschlagshöhe des j-ten Vortags
| |
| :C(j) = Faktor, der den Einfluss des j-ten Vortags beschreibt
| |
| | |
| Der Einfluss der Jahreszeit wird durch einen Jahresgang des Faktors C wiedergegeben.
| |
| | |
| :<math>C = 0.05 \cdot \sin(\frac{2 \pi}{365}) (i + 0.75 ) + 0.85</math>
| |
| | |
| :mit
| |
| :i = lfd. Tag des Abflussjahres
| |
| | |
| [[Bild:Theorie_Abb36.gif|thumb|Abbildung 36: Abhängigkeit des Abflussbeiwertes von der Vorgeschichte]]
| |
| | |
| Damit schwankt der Wert C zwischen <code>0,8 < C < 0,9</code>. Hierdurch wird erreicht, dass bei gleichem Vorregen zu unterschiedlichen Jahreszeiten unterschiedliche Vorregenindizes berechnet und damit eine veränderte Abflussbereitschaft in Rechnung gestellt wird.
| |
| | |
| In Abhängigkeit von der auf diese Weise quantifizierten Vorgeschichte kann unter Verwendung der gebietsspezifischen und für mittlere Vorfeuchteverhältnisse gültigen CN-Werte ein aktueller Abflussbeiwert berechnet werden. In [[:Bild:Theorie_Abb36.gif|Abbildung 36]] ist für unterschiedliche CN-Werte dargestellt, wie sich der aktuelle Abflussbeiwert in Abhängigkeit von der Vorgeschichte verändert.
| |
| | |
| [[Bild:Theorie_Abb37.gif|thumb|Abbildung 37: Abhängigkeit des Abflussbeiwertes von der kumulierten Niederschlagssumme]]
| |
| | |
| Da sich im Verlaufe eines Regenereignisses durch die Durchfeuchtung des Bodens die Abflussbereitschaft eines Einzugsgebiets verändert, wird ebenfalls eine Anpassung des Abflussbeiwertes während eines Ereignisses als Funktion der kumulierten Niederschlagshöhe vorgenommen. In [[:Bild:Theorie_Abb37.gif|Abbildung 37]] ist dieser Zusammenhang für unterschiedliche CN-Werte dargestellt.
| |
| | |
| Bei der Abhängigkeit der Abflussbereitschaft zum kumulierten Niederschlag bietet TALSIM 2.2 zwei Möglichkeiten:
| |
| | |
| # Variabler Verlustansatz (default):<br/>Die Anpassung eines Verlustwertes für die Funktion des Abflussbeiwertes zum kumulierten Niederschlag erfolgt für jeden Zeitschritt neu.<br/>(liefert insgesamt höhere Abflussbeiwerte, so dass auf die Berücksichtigung eines Vorregens verzichtet werden kann)
| |
| # Konstanter Verlustansatz:<br/>Die Anpassung des Verlustwertes erfolgt nur zu Ereignisbeginn einmalig.<br/>(der Ansatz eines Vorregens ist in diesem Fall zweckmäßig)
| |
| | |
| Welcher Ansatz bessere Ergebnisse liefert geht nur aus einem Vergleich mit gemessenen Ganglinien hervor. Grundsätzlich ergeben sich mit dem variablen Verlustansatz höhere Abflussspitzen und Füllen bei gleichen Bedingungen.
| |
| | |
| Eine weitere Möglichkeit zur Beeinflussung der Abflussbildung besteht in der Option, einen Endabflussbeiwert festzulegen. Damit beschränkt man unabhängig vom gewählten Verlustansatz den maximalen Abflussbeiwert. Standardmäßig setzt TALSIM den Endabflussbeiwert auf 1.
| |
| | |
| =====Bodenfeuchtesimulation=====
| |
| | |
| <u>Landnutzung:</u>
| |
| | |
| Bei der Anwendung der Bodenfeuchtesimulation ist die Angabe von Landnutzungen notwendig. Aus den Angaben zur Landnutzung wird die Durchwurzelungstiefe benötigt, um die Dicke der Durchwurzelungsschicht zu ermitteln. Weitere Parameter der Landnutzung, die zur Berechnung der Interzeption und der Transpiration dienen, sind:
| |
| | |
| * Wurzeltiefe
| |
| * Bedeckungsgrad
| |
| * Jahresgang des Bedeckungsgrades
| |
| * Blattflächenindex
| |
| * Jahresgang des Blattflächenindexes
| |
| | |
| Die Angabe von Haude-Faktoren zur besseren Berücksichtigung der Verdunstung je Landnutzung ist über Eingabe von Jahresgängen beliebig möglich und können den gewünschten Landnutzungen zugeordnet werden.
| |
| | |
| <u>Bodentyp / Bodenart:</u>
| |
| | |
| Die Bodenfeuchtesimulation basiert auf einer nichtlinearen Berechnung der einzelnen Bodenhorizonte. Der Boden wird dabei in verschiedene Horizonte (Schichten) eingeteilt. Jede Schicht wird berechnet und mit den (falls vorhanden) darunter bzw. darüber liegenden Schichten abgeglichen. Als Parameter zur Bodenfeuchteberechnung dienen folgende bodenphysikalischen Größen:
| |
| | |
| * Welkepunkt (WP)
| |
| * Feldkapazität (FK)
| |
| * Gesamtporenvolumen (GPV)
| |
| * Gesättigte Leitfähigkeit (k<sub>f</sub>-Wert)
| |
| * Maximale Infiltrationskapazität (Max.Inf.)
| |
| * Maximale Rate des Kapillaraufstiegs (Max.Kap.)
| |
| * Zuordnung zu einer Bodenart: Sand, Schluff, Ton
| |
| | |
| Die mögliche Anzahl der Bodenschichten läuft von minimal einer bis maximal sechs. Die Erfahrung zeigte, dass die besten Ergebnisse mit einer Aufteilung in drei Schichten erzielt werden konnten. Aus diesem Grund werden die eingegebenen Schichten programmintern immer in drei Horizonte unterteilt.
| |
| | |
| * Infiltrationsschicht (Standarddicke [cm] = 20)
| |
| * Durchwurzelte Schicht (Mindestdicke [cm] = 5)
| |
| * Transportschicht (Mindestdicke [cm] = 5)
| |
| | |
| Die Berechnung der neuen Bodenkennwerte für die programmintern verwendeten Schichten erfolgt durch eine Gewichtung entsprechend den vorgegebenen original Dicken der Schichten. Im Fall der gesättigten Leitfähigkeit läuft die Berechnung nach dem Prinzip der Erhaltung der Kontinuität der Strömung ab. Bei senkrechter Strömung soll aufgrund der Kontinuität der Strömung die Geschwindigkeit v bei gegebener Durchflussmenge in einer programminternen Schicht denselben Wert besitzen. Damit ist das hydraulische Gefälle nicht mehr konstant.
| |
| | |
| [[Bild:Theorie_Abb38.gif|thumb|Abbildung 38: Beispiel der Zusammenfassung von Bodenschichten anhand der
| |
| Durchwurzelungsschicht]]
| |
| | |
| :<math>k_{f,v} = \frac{\sum d}{\left ( \frac{d_1}{k_1} + \cdots + \frac{d_i}{k_i} + \cdots + \frac{d_n}{k_n} \right )}</math>
| |
| | |
| :mit
| |
| :d<sub>i</sub> = anteilige Schichtdicke der jeweiligen original Schicht [mm]
| |
| :k<sub>i</sub> = gesättigte Leitfähigkeit der jeweiligen original Schicht [mm/h]
| |
| :k<sub>f,v</sub> = gesättigte Leitfähigkeit der programmintern verwendeten Schicht [mm/h]
| |
| | |
| Die Zusammenfassung der Schichten ist in der [[:Bild:Theorie_Abb38.gif|Abbildung 38]] dokumentiert.
| |
| | |
| Alle mit der Bodenfeuchtesimulation berechneten Größen sind im nachfolgenden Bild angegeben.
| |
| | |
| [[Bild:Theorie_Abb39.gif|thumb|600px|center|Abbildung 39:Berechnete Größen mit der Bodenfeuchtsimulation]]
| |
| | |
| Auf der Basis der bereichsweisen linearen Abbildung der die Bodenfeuchte beeinflussenden Prozessfunktionen Infiltration, aktuelle Verdunstung (Evaporation + Transpiration), Perkolation, Interflow und Kapillaraufstieg wird für eine Bodenschicht die Wasserbilanzgleichung gelöst. Die Eingangsgröße für die Evaporation und Transpiration ermittelt sich aus der potentiellen Verdunstung:
| |
| | |
| Die zu lösende Gleichung ist:
| |
| | |
| [[Bild:Theorie_Abb39b.gif|thumb]]
| |
| | |
| :<math>\frac{d\theta(t)}{d\mbox{t}} = \mbox{Inf}(t) - \mbox{Perk}(t) - \mbox{Eva}_{akt}(t) - \mbox{Trans}_{akt}(t) - \mbox{Int}(t) + \mbox{Kap}(t)</math>
| |
| | |
| :mit:
| |
| :θ(t) = aktuelle Bodenfeuchte
| |
| :Inf(t) = Infiltration in den Boden
| |
| :Perk(t) = Perkolation (Durchsickerung)
| |
| :Eva<sub>akt</sub>(t) = aktuelle Evaporation
| |
| :Trans<sub>akt</sub>(t) = aktuelle Transpiration
| |
| :Int(t) = Interflow
| |
| :Kap(t) = Kapillaraufstieg
| |
| | |
| Infiltration, Perkolation, Evaporation, Transpiration, Interflow und Kapillaraufstieg sind von der aktuellen Bodenfeuchte abhängig. In der Simulation wird diese Abhängigkeit durch folgende Funktionsverläufe beschrieben.
| |
| | |
| :<math>\mbox{Inf}(\theta(t)) = \mbox{a}_v \cdot \left ( \mbox{GPV} - \theta(t) \right )^{1,4} + k_f</math>
| |
| :(Ansatz nach HOLTAN<ref name="holtan">'''Holtan, H.N.''' (1961): A Concept for Infiltration Estimates in Watershed Engineering, U.S. Department of Agriculture Publication, ARS 41-51.</ref>)
| |
| | |
| Der früher verwendete Ansatz:
| |
| | |
| :<math>\mbox{Perk}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \\ k_f \cdot \left ( \frac{\theta(t) - \left ( \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \right )}{\mbox{GPV} - \left ( \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \right )} \right )^{n_{PK}}, & \theta(t) > \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \end{cases}</math>
| |
| :(mod. Ansatz nach OSTROWSKI, 1992<ref name="ostrowski_1992">'''Ostrowski, M.''' (1992): Ein universeller Baustein zur Simulation hydrologischer Prozesse, Wasser und Boden, Heft 11 ({{file|pdf|Ostrowski_1992_Universeller_Baustein.pdf|PDF}})</ref>, BEAR, 1988<ref name="bear_1988">'''Bear, J.''' (1988): Dynamics of fluids in porous media, American Elsevier Environmental Science Series ([http://books.google.com/books?hl=en&lr=&id=lurrmlFGhTEC&oi=fnd&pg=PP9&sig=GZbr6T5bMHLmCFUNorn3bd_DPV4 books.google.com])</ref>)
| |
| | |
| wurde '''''in TALSIM 2.2''''' zu Gunsten eines Ansatzes nach VAN GENUCHTEN<ref>'''van Genuchten, M. Th.''' (1980): A closed-fom equation for predicting the hydraulic conductivity of unsaturated soils - Soil Science Society of America Journal, 44, pp 892-898 ({{SERVER}}/wiki/images/icons/pdf.gif [http://hydro.nevada.edu/courses/gey719/vg.pdf PDF])</ref> geändert.
| |
| | |
| :<math>\mbox{Perk}(\theta(t)) = k_f \cdot \theta_e^a \cdot \left [ 1 - \left ( 1 - \theta_e^{\frac{n_{PK}}{n_{PK}-1}} \right )^{\frac{n_{PK}-1}{n_{PK}}} \right ]^2 \quad \quad \quad \quad \mbox{mit} \quad a = 0,5</math>
| |
| | |
| :<math>\theta_e = \frac{\theta(t)-\mbox{WP}}{\mbox{GPV}-\mbox{WP}}</math>
| |
| | |
| :(Ansatz nach Wösten und van Genuchten, 1988<ref>'''Wösten, J.H.M., Van Genuchten, M.''' (1988): Using texture and other soil properties to predict the unsaturated soil hydraulic functions, Soil Science Society of America Journal ({{SERVER}}/wiki/images/icons/pdf.gif [http://www.ars.usda.gov/SP2UserFiles/Place/53102000/pdf_pubs/P1040.pdf PDF])</ref>, BENECKE, 1992<ref>'''Benecke, P.''' (1992): Gedanken zur Waldbodenrestaurierung mit Bodenbearbeitung, [http://pica1l.lhb.tu-darmstadt.de/CHARSET=ISO-8859-1/DB=LHBDA/FKT=6015/FRM=%2BNUM%2B0002-5860/IMPLAND=Y/LNG=DU/LRSET=1/MAT=9001%2505TP%2505%2506/SET=1/SID=f68514bd-1/SRT=YOP/TTL=1/SHW?FRST=1 Allg. Forst Zeitschr.], 47:542-545 <span style="color:red;">???</span></ref>.
| |
| | |
| :<math>\mbox{Eva}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{WP} \\ \mbox{f}_{Eva} \cdot \left ( \frac{\theta(t)-\mbox{WP}}{\mbox{GPV}-\mbox{WP}} \right ), & \theta(t) > \mbox{WP} \end{cases}</math>
| |
| | |
| :<math>\mbox{Trans}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP} \\ \mbox{f}_{TP} \cdot \left ( \frac{\theta(t) - \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP}}{\mbox{GPV} - \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP}} \right )^{n_{TP}}, & \theta(t) > \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP} \end{cases}</math>
| |
| | |
| [[Bild:Theorie_Abb40.gif|thumb|500px|Abbildung 40: Darstellung ausgewählter Bodenprozessfunktionen]]
| |
| | |
| :mit:
| |
| :a<sub>v</sub> = Infiltrationsfaktor nach Holtan<ref name="holtan" /> (in TALSIM <code>a<sub>v</sub> = 1</code>)
| |
| :k<sub>f</sub> = Durchlässigkeitsbeiwert des gesättigten Bodens
| |
| :nFK = nutzbare Feldkapazität (<code>nFK = FK - WP</code>)
| |
| :WP = Welkepunkt
| |
| :FK = Feldkapazität
| |
| :GPV = gesamtes Porenvolumen
| |
| :f<sub>PK</sub> = bodenabhängiger Skalierungsfaktor der Perkolationsfunktion
| |
| :n<sub>PK</sub> = bodenabhängiger Krümmungsparameter der Perkolationsfunktion
| |
| :f<sub>Eva</sub> = bodenabhängiger Skalierungsfaktor der Evaporationsfunktion
| |
| :f<sub>TP</sub> = bodenabhängiger Skalierungsfaktor der Transpirationsfunktion
| |
| :n<sub>TP</sub> = Krümmungsparameter der Transpirationsfunktion
| |
| | |
| Die Programmparameter werden intern berechnet. Der Anwender muss lediglich die Bodenkennwerte k<sub>f</sub>, WP, FK und GPV angeben.
| |
| | |
| Die Simulation erfolgt mit einem neu entwickelten Baustein zur Simulation von Speichern, deren Prozessfunktionen bereichsweise linear abzubilden sind. Der Baustein ist eine Weiterentwicklung des Ansatzes von Ostrowski, 1992<ref name="ostrowski_1992" /> und wird detailliert bei Mehler, 2000<ref name="mehler_2000">'''Mehler, R.''' (2000): Mischwasserbehandlung - Verfahren und Modellierung, Mitteilungen des Instituts für Wasserbau und Wasserwirtschaft der TU Darmstadt, Heft 113 (siehe auch Zusammenfassung {{file|pdf|Mehler_1998_Mathematische_Herleitung.pdf|PDF}})</ref> beschrieben. Er ermöglicht die simultane Lösung der Kontinuitätsgleichung für mehrere Prozesse ohne aufwendige Iterationen und wird nachfolgend kurz erläutert.
| |
| | |
| Für einen Speicher, dessen Inhalt von mehreren Zu- bzw. Ablaufprozessen abhängig ist, kann die Kontinuitätsgleichung wie folgt dargestellt werden:
| |
| | |
| :<math>\frac{\mbox{d}S(t)}{\mbox{d}t} = \sum_{j=1}^m Q_{zu,j}(t) - \sum_{i=1}^n Q_{ab,i}(t)</math>
| |
| | |
| :mit:
| |
| :S(t) = Speicherinhalt des Speichers
| |
| :Q<sub>zu,j</sub>(t) = Zulaufprozess
| |
| :Q<sub>ab,i</sub>(t) = Ablaufprozess
| |
| :m = Anzahl der Zulaufprozesse
| |
| :n = Anzahl der Ablaufprozesse
| |
| | |
| Die Entnahmeterme sind in der Regel nichtlineare Funktionen des Speicherinhaltes (z.B. die Entnahme aus dem Bodenspeicher mit den Prozessfunktionen).
| |
| | |
| Diese Funktionen werden bereichsweise linearisiert.
| |
| | |
| :<math>y(t) = A \cdot \left ( \frac{y_{i+1}-y_i}{S_{i+1}-S_i} \cdot (S(t)-S_i) + y_i \right ) \quad \quad \quad \mbox{mit} \quad A = A_1 \cdot A_l \cdot A_{l+1} \cdot \ldots \cdot A_{p-1} \cdot A_p</math>
| |
| | |
| :mit:
| |
| :y(t) = Entnahme aus dem Speicher
| |
| :S(t) = Speicherinhalt
| |
| :y<sub>i</sub> = Größe der Entnahme an der Stützstelle i
| |
| :S<sub>i</sub> = Speicherinhalt an der Stützstelle i
| |
| :A = Multiplikator der Prozessgröße als Produkt aller weiteren Abhängigkeiten
| |
| :p = Anzahl weiterer Abhängigkeiten
| |
| | |
| [[Bild:Theorie_Abb41.gif|thumb|Abbildung 41: Bereichsweise linearisierte Entnahmefunktion]]
| |
|
| |
|
| Für jede Entnahmefunktion kann nach Linearisierung eine Geradengleichung aufgestellt werden, die nur noch vom Speicherinhalt abhängig ist. Die Steigung "m" der Geraden ändert sich von Stützstelle zu Stützstelle.
| | Trough loss (MV) is set by the user in the [[ALL-Datei|ALL-File]]. |
|
| |
|
| Somit gibt es für jede vom Speicherinhalt abhängige Funktion ein bereichsweise linearisierter Verlauf entlang der Speicherfüllung. Die Funktion selbst kann mit einem für jeden Zeitschritt konstanten Faktor (A) skaliert werden, der alle weiteren Abhängigkeiten als Produkt zusammenfasst.
| | The trough loss is the mean value for an inclined surface. Due to the fact that troughs are not evenly distributed and experience has shown that run-off occurs before all troughs are completely filled the following assumption is made, that: |
|
| |
|
| Die Kontinuitätsgleichung kann nun umformuliert werden zu:
| | [[File:Theorie_Abb35.gif|thumb|Abbildung 35: Schematic of the model approach for wetting and trough losses]] |
|
| |
|
| :<math>\frac{\mbox{d}S}{\mbox{d}t} = \sum_{j=1}^m Q_{z,j}(t) + \sum_{k=1}^m y_{k,i} + \sum_{k=1}^m m_{k,i} \cdot (S(t)-S_i)</math>
| | * 1/3 of the impervious area has a reduced trough loss of 1/3 MV |
| | * 1/3 of the impervious area has a mean trough loss of 3/3 MV |
| | * 1/3 of the impervious area has a elevated trough loss of 5/3 MV |
|
| |
|
| :<math>\frac{\mbox{d}S}{\mbox{d}t} = \sum_{j=1}^m Q_{z,j}(t) + \sum_{k=1}^m y_{k,i} + \mbox{C}_2 \cdot (S(t)-S_i) \quad \quad \quad \mbox{mit} \quad \mbox{C}_2 = \sum_{k=1}^m m_{k,i}</math>
| | . Therefore run-off occurs as soon as the rainfall (reduced by evaporation) is greater than wetting losses and 1/3 of the trough losses (in dry antecedent conditions). In [[:File:Theorie_Abb35.gif|Abbildung 35]] the assumptions are depicted schematically. |
|
| |
|
| Nach Ausmultiplizieren der Klammer wird die Kontinuitätsgleichung zu:
| | The run-off coefficient of the impervious areas (after overcoming initial losses) is set to ψ = 1. When determining the fraction of impervious areas for a catchment it needs to be considered that not all paved or impervious areas drain into the canalization. |
|
| |
|
| :<math>\frac{\mbox{d}S}{\mbox{d}t} + \mbox{C}_2 \cdot S(t) = \mbox{C}_1 \quad \quad \quad \mbox{mit} \quad \mbox{C}_1 = \sum_{j=1}^m Q_{z,j}(t) + \sum_{k=1}^m y_{k,i} + \mbox{C}_2 \cdot S_i</math>
| | Wetting and trough losses are continuously made available through the ongoing balancing of these reservoirs and evaporation. |
|
| |
|
| Diese Gleichung ist eine inhomogene lineare Differentialgleichung erster Ordnung und besitzt folgende Lösung:
| |
|
| |
|
| :<math>S(t) = \frac{\mbox{C}_2}{\mbox{C}_1} \cdot (1-e^{-C_1 \cdot t}) + S_0 \cdot e^{-C_1 \cdot t} \quad \quad \quad \mbox{mit} \quad S_0 = S(t=0)</math>
| | ===Surface water reservoir content (fraction of pervious areas) O=== |
|
| |
|
| Damit steht die Speicherfüllung zu jedem Zeitpunkt fest. Tritt innerhalb eines Zeitintervalls eine Bereichsüberschreitung ein, sind die Größen C1 und C2 mit den jeweils aktuellen Steigungen und Achsenabschnittswerten der bereichsweise linearisierten Funktionen neu zu berechnen. Die simultane Berechnung der Abgabenfunktionen wird durch Einsetzen der Speicherinhaltsgleichung in die jeweilige Geradengleichung erreicht.
| | Surface water reservoir content is determined through the ongoing balancing of a loss reservoir in dependency of the chosen run-off generation approach.Details can be found in the following sections about calculation of infiltration respectively run-off generating rainfall. |
|
| |
|
| Allgemein ausgedrückt gilt für die mittlere Intensität aller Abgaben:
| | ===Infiltration respectively run-off generating rainfall I(t), Nw(t)=== |
|
| |
|
| :<math>\bar{y} = \frac{1}{\Delta t} \int_{t=0}^{\Delta t} A \cdot \left [ y_i \cdot S_i + m_i \cdot \left ( \frac{C_2}{C_1} \cdot ( 1 - e^{-C_1 \cdot t} ) + S_0 \cdot e^{-C_1 \cdot t} \right ) \right ]</math> | | Infiltration into the soil can not be neglected for pervious areas due to the fact that infiltration substantially influences run-off. Three approaches were implemented in the model for the calculation of infiltration: |
|
| |
|
| :<math>\bar{y} = y_i + m_i \cdot \left [ -S_i + \frac{C_2}{C_1} + (1-e^{-C_1 \cdot \Delta t}) \cdot \left ( \frac{S_0}{\Delta t \cdot C_1} - \frac{C_2}{\Delta t \cdot C_1^2} \right ) \right ]</math>
| | # constant run-off coefficient ψ |
| | # event specific run-off coefficient similar to the method of the Soil-Conservation-Service (SCS) |
| | # soil moisture simulation |
|
| |
|
| Mit diesem Berechnungsschema können alle Speicher, deren Prozesse bereichsweise linear zu beschreiben sind, berechnet werden. In TALSIM werden mit diesem Baustein die Bodenprozesse, die Speicher sowie die Transportstrecken berechnet.
| | ====constant run-off coefficient ψ==== |
|
| |
|
| [[Bild:Theorie_Abb42.gif|thumb|Abbildung 42: Aufteilung eines Einzugsgebietselementes in Elementarflächen]]
| | By supplying a ψ<sub>u</sub>-value the remaining rainfall after having covered the initial losses (wetting and trough losses)generates run-off according to the ratio of the run-off coefficient ψ<sub>u</sub> independent of previous history and the characteristics of the rainfall (height, intensity, duration). If possible this approach should not be used, because it only represents a very rudimentary description of the run-off generation process. |
|
| |
|
| <u>Elementarflächen:</u>
| |
|
| |
|
| Wird mit der Bodenfeuchtesimulation die Abflussbildung berechnet, wird gleichzeitig das Elementarflächenkonzept angewandt. Ein Einzugsgebietselement wird dabei in beliebig viele hydrologisch homogene Flächen unterteilt.
| | ====SCS-Method==== |
| | :''refer to [[SCS-Verfahren|SCS-Method]]'' |
|
| |
|
| [[Bild:Theorie_Abb43.gif|thumb|left|Abbildung 42: Zuordnung von Bodentyp und Landnutzung zu Elementarflächen]] | | ====Soil moisture simulation==== |
| | :''refer to [[Bodenfeuchtesimulation|Soil moisture simulation]]'' |
|
| |
|
| Für jede Elementarfläche gilt die gezeigte Zuordnung von Landnutzung und Bodentyp. Die aus einer Elementarfläche resultierende Wassermenge wird am Elementausgang angesetzt, d.h. alle Elementarflächen geben unabhängig ihrer Lage im Einzugsgebiet Wasser mit der gleichen zeitlichen Verzögerung ab.
| | ==Run-off concentration== |
| | [[File:Parallelspeicherkaskade_EZG.gif|thumb|400px|Abbildung 44: Calculation of run-off concentration for rural catchments]] |
| | Run-off concentration determines the delay of discharge out of the catchment. Calculation of Interflow and base flow is dependent on the chosen calculation approach. If [[Bodenfeuchteberechnung|soil moisture simulation]] is chosen, the discharge of both run-off components at the catchment outlet is delayed through a linear reservoir. If the run-off coefficient approach or the SCS-Method is chosen, interflow is neglected and base flow is determined through regarding the given specific base discharge and a possible consideration of an annual pattern. |
|
| |
|
| Die Berechnung der Bodenfeuchte ist sehr rechen- und damit auch zeitintensiv. Dies gilt insbesondere dann, wenn viele Elementarflächen je Teilgebiet eingerichtet sind. In TALSIM 2.2 besteht jetzt die Möglichkeit Elementarflächen programmintern aggregieren zu lassen, d.h. nach Vorgabe eines Grenzwertes werden alle Elementarflächen, deren Flächenanteil am Teilgebiet kleiner als der Grenzwert ist zu einer Elementarfläche flächengewichtet zusammengefasst. Dies ist besonders dann sinnvoll, wenn viele Elementarflächen mit Anteilen unter 5% vorhanden sind.<br clear="all"/>
| | A parallel reservoir cascade is utilized with two reservoirs each for the cascade for pervios and the cascade for impervious areas. |
| | The reservoir cascades can be calculated as linear or [[Speicherbaustein|non-linear reservoirs]]. If the reservoir cascade parameters are not supplied, they are calculated through using area characteristics according to {{:Literatur:Zaiß 1986}} |
|
| |
|
| [[Bild:Parallelspeicherkaskade.gif|thumb|Abbildung 44: Berechnung der Abflusskonzentration von Einzugsgebieten]]
| |
|
| |
|
| ===Abflusskonzentration=== | | ==Literature== |
| | <references/> |
|
| |
|
| Die Abflusskonzentration bestimmt die Verzögerung des Oberflächenabflusses aus dem Einzugsgebiet. Es wird eine Parallelspeicherkaskade mit drei Speichern für unbefestigte und eine Kaskade für befestigte Flächen benutzt. Der Abfluss der Komponenten Interflow und Grundwasser wird über einen linearen Einzelspeicher verzögert an den Elementausgang abgegeben.
| | [[Category:BlueM Theorie]] |
The natural process leading from rain to run-off is divided into three phases. The phases are Belastungsbildung, run-off generation (bzw. Belastungsaufteilung) and run-off concentration. The calculation approach for each of these phases is described in the following sections of this article.
Belastungsbildung
Die Belastungsbildung describes the determination of an areal rainfall for the considered catchment.Rainfall data is imported into BlueM via external time series. Therefore no explicit calculations are necessary for this phase.
Run-off generation
In this phase surface run-off, infiltration, evaporation and interflow are determined by calculating the effective rainfall out of the fallen rain. Snow is calculated for temperatures below 0°C. The Snow-Compaction-Method Knauf[1] is applied.
Rainfall (system load) is divided into rainfall which directly generates run-off and run-off diminishing losses (wetting, trough, evaporation and infiltration losses). Therefore this phase is also called the Belastungsaufteilung. The mathematical equation for the momentary Belastungsaufteilung is as follows:
- [math]\displaystyle{ Nw(t) = N(t) - VP(t) - I(t) - \frac{dO}{dt} - \frac{dS}{dt} }[/math]
- mit:
- NW = run-off generating rainfall
- N = rainfall
- VP = potential evaporation
- I = infiltration into the soil
- O = surfacce water reservoir content
- S = snow reservoir content
The individual elements of the equation and the calculation of these elements is described in the following.
Rainfall N(t)
BlueM requires rainfall data in form of rain time series. In general is does not matter if a block rain, Regenspektrum or a longtime rainfall time series. Depending on the purpose of the simulation the appropriate load (type) must be chosen. Rainfall time series originate out of the BlueM time series management or are created immediately before simulation begin as is the case for short term prediction by supplying a rainfall duration, rainfall height and choosing a model rainfall .
Evaporation VP(t)
There are two possibilities for the input of potential evaporation:
a) annual evaporation
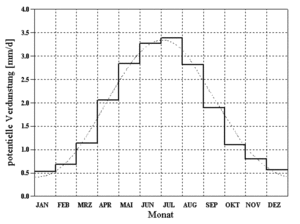
Abbildung 33: annual pattern of potential evaporation according to Brandt (1979)
[2]A normed annual pattern of potential evaporation according to Brandt[2] is utilized for the calculation of potential evaporation. Through the evaluation of measurements from twenty different stations, whichs mean-values are depicted as a histogram in Abbildung 33, the following smoothing function was derived (doted line in Abbildung 33):
- [math]\displaystyle{ VP[\mbox{mm/d}] = \begin{cases}(0.96 + 0.0033 \cdot i) \cdot \sin(\frac{2 \pi}{365})(i - 148) + 1.58, & i \lt = 300 \\ 2.56 - 1.53 / 65. \cdot (i - 300.), & i \gt 300 \end{cases} }[/math]
- ´with
- i = ongoing day of the hydrological year
- i = 1 → 1. November
Potential evaporation according to Brandt refers to grass reference evaporation[3] and assumes an annual total evaporation loss of 654,282 mm. If a different annual total evaporation loss is entered, the value determined by Brandt is scaled accordingly.
b) evaporation time series
If a evaporation time series is supplied the utilized time step is imported.
Attention: For time steps < 1 day the time series value is additionally overprinted with a daily pattern! (Bug 1)
daily pattern of evaporation

Abbildung 34: Daily pattern of potential evaporation as a multiple of mean daily evaporation
If the chosen time step for the calculation is < 1 day the potential evaporation for each time step is calculated by taking the daily pattern depicted in Abbildung 34 into consideration. If the chosen time step is ≥ 1 day the daily pattern is disregarded.
Surface water reservoir content(fraction of impervious area) O
Snow reservoir content as well as infiltration can be neglected for impervious areas. Therefore the equation of balance is reduced to:
- [math]\displaystyle{ Nw(t) = N(t) - VP(t) - \frac{dO}{dt} }[/math]
in which the change in surface water reservoir content dO/dt represents wetting of the surface as well as filling and depletion of water (through evaporation) in troughs.
The wetting loss (BV) for impervious areas is set to the following standard value.
BV = 0.5 mm
Trough loss (MV) is set by the user in the ALL-File.
The trough loss is the mean value for an inclined surface. Due to the fact that troughs are not evenly distributed and experience has shown that run-off occurs before all troughs are completely filled the following assumption is made, that:
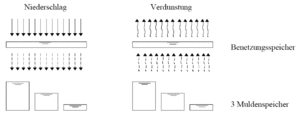
Abbildung 35: Schematic of the model approach for wetting and trough losses
- 1/3 of the impervious area has a reduced trough loss of 1/3 MV
- 1/3 of the impervious area has a mean trough loss of 3/3 MV
- 1/3 of the impervious area has a elevated trough loss of 5/3 MV
. Therefore run-off occurs as soon as the rainfall (reduced by evaporation) is greater than wetting losses and 1/3 of the trough losses (in dry antecedent conditions). In Abbildung 35 the assumptions are depicted schematically.
The run-off coefficient of the impervious areas (after overcoming initial losses) is set to ψ = 1. When determining the fraction of impervious areas for a catchment it needs to be considered that not all paved or impervious areas drain into the canalization.
Wetting and trough losses are continuously made available through the ongoing balancing of these reservoirs and evaporation.
Surface water reservoir content (fraction of pervious areas) O
Surface water reservoir content is determined through the ongoing balancing of a loss reservoir in dependency of the chosen run-off generation approach.Details can be found in the following sections about calculation of infiltration respectively run-off generating rainfall.
Infiltration respectively run-off generating rainfall I(t), Nw(t)
Infiltration into the soil can not be neglected for pervious areas due to the fact that infiltration substantially influences run-off. Three approaches were implemented in the model for the calculation of infiltration:
- constant run-off coefficient ψ
- event specific run-off coefficient similar to the method of the Soil-Conservation-Service (SCS)
- soil moisture simulation
constant run-off coefficient ψ
By supplying a ψu-value the remaining rainfall after having covered the initial losses (wetting and trough losses)generates run-off according to the ratio of the run-off coefficient ψu independent of previous history and the characteristics of the rainfall (height, intensity, duration). If possible this approach should not be used, because it only represents a very rudimentary description of the run-off generation process.
SCS-Method
- refer to SCS-Method
Soil moisture simulation
- refer to Soil moisture simulation
Run-off concentration
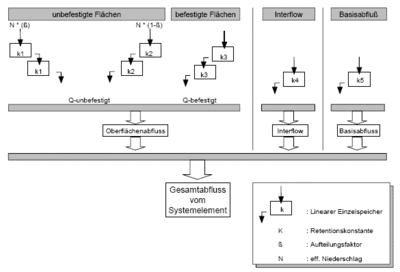
Abbildung 44: Calculation of run-off concentration for rural catchments
Run-off concentration determines the delay of discharge out of the catchment. Calculation of Interflow and base flow is dependent on the chosen calculation approach. If soil moisture simulation is chosen, the discharge of both run-off components at the catchment outlet is delayed through a linear reservoir. If the run-off coefficient approach or the SCS-Method is chosen, interflow is neglected and base flow is determined through regarding the given specific base discharge and a possible consideration of an annual pattern.
A parallel reservoir cascade is utilized with two reservoirs each for the cascade for pervios and the cascade for impervious areas.
The reservoir cascades can be calculated as linear or non-linear reservoirs. If the reservoir cascade parameters are not supplied, they are calculated through using area characteristics according to Zaiß (1986)[4]
Literature
- ↑ Knauf, D. (1980): Die Berechnung des Abflusses aus einer Schneedecke, in: DVWK-Schriften, Heft 46, Analyse und Berechnung oberirdischer Abflüsse PDF

- ↑ 2.0 2.1 Brandt, T. (1979): Modell zur Abflussgangliniensimulation unter Berücksichtigung des grundwasserbürtigen Abflusses, Technischer Bericht Nr. 24 aus dem Institut für Wasserbau, Fachgebiet Ingenieurhydrologie und Hydraulik der TH Darmstadt
- ↑ DVWK (Hrsg.) (1996): Ermittlung der Verdunstung von Land- und Wasserflächen, DVWK-Merkblätter zur Wasserwirtschaft, Heft 238. Bonn: Wirtschafts- und Verlagsgesellschaft Gas und Wasser mbH
- ↑ Zaiß, H. (1986): Abflussermittlung aus Teilflächen, in "Hydrologische Abflussmodelle in der praktischen Anwendung", 36. Fortbildungslehrgang des BWK-Hessen am 21. März 1986, Friedberg [ihwb-Bibliothek: Inv.-Nr. 5593, 10 BWK 36] PDF
 OCR
OCR 
![]() BlueM.Sim | Download | Application | Theory | Development
BlueM.Sim | Download | Application | Theory | Development


 OCR
OCR 


