SCS-Method

BlueM.Sim | Downloads | Application | Theory | Development

BlueM.Sim theory

Table of Contents

• Einleitung
• Modellierungstechnische Grundlagen
  • Begriffsdefinitionen
  • Programmstruktur und Datenhaltung
  • Bildung der Zuflussbelastung
  • Berechnungsreihenfolge
  • Simulation types
  • Time series management
• Hydrological Basics
  • Rural Catchments
    • Soil moisture calculation
    • SCS-Method
  • Urban Catchments
  • Individual discharges
  • Transport elements
  • Consumers
  • Branching points
  • Talsperren
    • Betriebsregelkonzept
    • Grundlegende Typen von Betriebsregeln
    • Grundsätze zur Beschreibung von Betriebsregeln
    • Umsetzung der Gesetzmäßigkeiten für die Simulation
    • Anwendung an einem Beispiel
  • Storm-water overflows
  • Regenüberlaufbecken
• Systemübergreifende hydrologische Methoden
  • Speicherbaustein
  • Systemzustände
    • Steuern und Regeln

Event specific run-off coefficient on the basis of the Curve-Number-Method (CN-Method)of the Soil-Conservation-Service (SCS)

Theory

The Method applied in BlueM is a further development of the CN-Method (USDA (1964)) by Zaiß (1989)

Abbildung 36: Dependency of the run-off coefficient on previous history

By supplying a soil type and land use dependent CN (refer toDVWK (1991)) an antecedent dependent initial loss as well as an antecedent dependent relationship of the run-off coefficient on the accumulated amount of rain up to a desired point in time can be determined. This results in an increasing run-off coefficient due to the accumulating rain amount in the course of a rainfall event.

A current run-off coefficient can be determined in dependency of the quantified previous history, as described above, by using the area specific and for average antecedent moisture conditions (AMC) (USDA (1964)) valid CN. In Abbildung 36 the development of the run-off coefficient depending on previous history is depicted for different CN.

Abbildung 37: Dependency of the run-off coefficient on the accumulated amount of rain

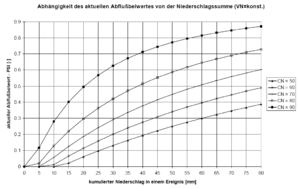
As soil moisture increases during the course of a rainfall event the conditions for run-off development change which is why the run-off coefficient is additionally adjusted during a rainfall event as a function of accumulated rain. This correlation is depicted for different CN in Abbildung 37.

Attention

The CN-Method was developed for the simulation of solitary events on a daily basis. A further development is being undertaken for continuous simulation with smaller time steps.(refer to Bug 23 and Discussion)

Calculation

one-time calculated parameters

Input: CNII

Die Umrechnung von CNII in CNI bedeutet, dass davon ausgegangen wird, dass das Gebiet zu Beginn der Simulation trocken ist?!

Conversion of CNII to CNI:

[math]\displaystyle{ CN_I = \frac{CN_{II}}{(2.3340 - 0.01334 \cdot CN_{II})} }[/math]

Maximum retention capability of the area (storage capacity) Smax [mm]:

[math]\displaystyle{ S_{max} = \frac{25400}{CN_I} - 254 }[/math]

area specific initial loss Ia [mm]:

[math]\displaystyle{ I_a = a \cdot S_{max} }[/math]

with

a = constant, originally set to 0,2 , adjusted to European conditions in BlueM as 0,05

Krümmungsparameter CVW:

Laut Sartor, der die selbe Gleichung verwendet, stammt dieser Ansatz aus der Dokumentation von SMUSI 3.0

[math]\displaystyle{ CVW = \frac{-100.}{\ln(\frac{0.5}{I_a})} }[/math]

entspricht b1 in Gl. 4.5b in Zaiß (1989)

laut Zaiß:

Eine Abhängigkeit des "Krümmungsparameters" b₁ von Gebietskenngrößen konnte im Rahmen dieser Arbeit nicht gefunden werden. Sie läßt sich nach den hier aufgeführten Zusammenhängen lediglich über Regressionsanalysen mehrerer N-A-Ereignisse für das jeweils betreffende Einzugsgebiet ermitteln.

continuously calculated parameters

previous history

Previous history is quantified through the 21-day-antecedent rain index VN:

[math]\displaystyle{ V_N = \sum_{j=0}^{21} C(j)^j \cdot h_{N,j} }[/math]

Gl. 2.1 in Zaiß (1989)

with

hN,j = rain height of the preceding day j (j = 0 is the current day)

C(j) = factor, which describes the influence of the preceding day j

Seasonal influence is considered through the annual pattern of factor c.

[math]\displaystyle{ C = 0.85 \cdot \sin\left(\frac{2 \pi}{365}\right) (i + 0.75 ) + 0.85 }[/math]

Quelle? bei Zaiß finden sich nur so ähnliche Formeln (2.2 & 2.3)

with

i = ongoing day of the hydrological year

C will alternate between 0,8 < C < 0,9. This allows for different antecedent rain indices due to seasonal differences for same antecedent rain amounts and thereby leads to different conditions for run-off development.

Event dependent initial loss

[math]\displaystyle{ h_{va} = I_a \cdot e^{-\frac{V_N}{CVW}} }[/math]

Gl. 4.5b in Zaiß (1989)

run-off coefficient

Dependency of ψ on hva and hNE (withAv = 0.05)

[math]\displaystyle{ \psi = \begin{cases} 0, & h_{va} \ge h_{NE} \\ 1 - \left(\frac{h_{va}}{A_v \cdot h_{NE} + (1 - A_v) \cdot h_{va}}\right)^2, & h_{va} \lt h_{NE} \end{cases} }[/math]

Gl. 4.4 in Zaiß (1989)

with

Av = loss ratio = 0,05

hNE = event-driven sum of rainfall [mm]