Soil moisture calculation

BlueM.Sim | Download | Application | Theory | Development

BlueM.Sim theory

Table of Contents

• Einleitung
• Modellierungstechnische Grundlagen
  • Begriffsdefinitionen
  • Programmstruktur und Datenhaltung
  • Bildung der Zuflussbelastung
  • Berechnungsreihenfolge
  • Simulation types
  • Time series management
• Hydrological Basics
  • Rural Catchments
    • Soil moisture calculation
    • SCS-Method
  • Urban Catchments
  • Individual discharges
  • Transport elements
  • Consumers
  • Branching points
  • Talsperren
    • Betriebsregelkonzept
    • Grundlegende Typen von Betriebsregeln
    • Grundsätze zur Beschreibung von Betriebsregeln
    • Umsetzung der Gesetzmäßigkeiten für die Simulation
    • Anwendung an einem Beispiel
  • Storm-water overflows
  • Regenüberlaufbecken
• Systemübergreifende hydrologische Methoden
  • Speicherbaustein
  • Systemzustände
    • Steuern und Regeln

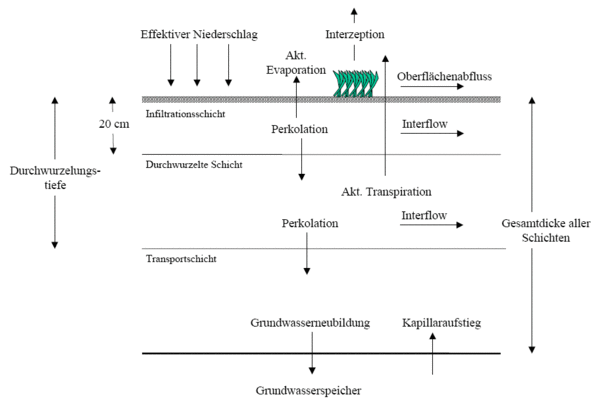
All process-values which are calculated through soil moisture simulation are depicted in the following picture.

Abbildung 39: calculated process-values through soil moisture simulation

Hydrological Response Units (HRUs)

Abbildung 42: Sectioning of a catchment into HRUs

If Runoff is determined through soil moisture simulation, the HRU concept is applied. This results in a catchment being sub-sectioned into a various amount of hydrological homogenous areas.

Abbildung 43: Assignment of soil type and land use to a HRU

The depicted assignment of land use and soil type is valid for each HRU. The resulting amount of water out of a HRU is applied at the outlet of the elemt. Therefore all HRUs discharge their Water with the same time delay, independent of their position within the catchment.

Soil moisture calculation is computationally intensive and therefore very time-consuming. This is especially true if there are many HRUs in each sub-catchment.

Land use

Providing information on land use is necessary to run the soil moisture calculation. E.g. the thickness of the rooted zone is determined by providing the root depth in the information regarding land use. Furthermore the parameters of land use are needed to calculate interception and transpiration. The parameters are:

• root depth
• soil coverage
• annual pattern of soil coverage
• leaf area index
• annual pattern of the leaf area index

Providing Haude-Coefficients is possible by providing an annual pattern and assigning them to the desired land use. This allows for a better consideration of evaporation for each land use.

These Haude-Coefficients scale the valid potential grass reference-evaporation for the time step by their ratio to the corresponding Haude-Coefficient for grass.

Soil type

The soil moisture simulation is based on the non-linear calculation of the individual soil layers. The soil is divided into different soil layers with different soil textures. Each layer is simulated individually and interacts with the layers above or below. The parameters for the soil moisture calculation are the following physical soil properties for the soil textures of each individual layer:

• wilting point (WP)
• field capacity (FK)
• total pore volume (GPV)
• saturated hydraulic-conductivity (kf-Wert)
• maximum infiltration capacity (MaxInf)
• maximum rate of capillary rise (MaxKap)
• Assignment to a soil category: sand, silt, clay

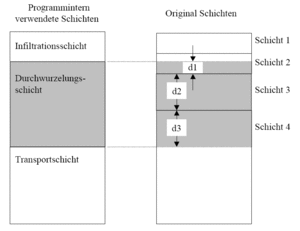
As few as one or as many as six soil layers can be entered. A division into three layers has proven to yield the best results. That is why the entered layers are always transformed into three calculation layers in BlueM internally.

• infiltration layer (standard thickness = 20 [cm])
• root layer (minimum thickness = 5 [cm])
• transport layer (minimum thickness = 5 [cm])

Abbildung 38: Example of the aggregation of soil layers for the root layer

The new characteristic soil parameters for the internally used layers are calculated by weighting the original parameters of the original layers according to the original thickness of these layers. Saturated hydraulic conductivity is calculated according to conservation of continuity of the flow. For vertical flow the velocity v is to be constant within a layer for a given flow due to the continuity of the flow. Therefore the hydraulic gradient is no longer constant.

[math]\displaystyle{ k_{f,v} = \frac{\sum d}{\left ( \frac{d_1}{k_1} + \cdots + \frac{d_i}{k_i} + \cdots + \frac{d_n}{k_n} \right )} }[/math]

with

di = depth of each original layer [mm]

ki = saturated hydraulic conductivity of each original layer [mm/h]

kf,v = saturated hydraulic conductivity of the internally used layer [mm/h]

The aggregation of the layers is depicted in Abbildung 38.

Interception

In BlueM the inflow to the interception reservoir (QzuIC) is described as a linear function of the free interception reservoir.

[math]\displaystyle{ Q_{zu_{IC}} = k_{IC} \cdot ( \mbox{IC}_{max} - \mbox{IC}_{akt}) }[/math]

with:kIC = 10.0 = Parameter to describe the fill rate of the interception reservoir [1/h] (Bug 409)

The maximum interception capacity for agricultural crops according to von Hoyningen-Huene (1983) is:

[math]\displaystyle{ \mbox{IC}_{max} = 0.935 + 0.498 \cdot LAI - 0.00575 \cdot LAI^2 }[/math]

with

LAI = Leaf Area Index [-]

The rate of evaporation is assumed to be equal to the rate of potential evaporation (= ETp). A simple differential equation can be derived due to the fact that inflow is equal to the amount of rain above the vegetation minus the rain which penetrates it :

[math]\displaystyle{ \frac{\mbox{dIC}}{\mbox{d}t} = k_{IC} \cdot ( \mbox{IC}_{max} - \mbox{IC}(t)) - ET_p }[/math]

Therefore the amount of penetrating rain can be determined through the subtraction of interception from rainfall onto the vegetation.

To simplify things it is assumed that this approach is valid for wooded areas, although this approach was derived out of studies for agricultural crops.

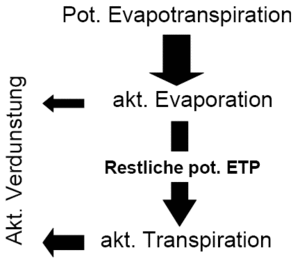
Furthermore the interception evaporation is calculated, which is subtracted from the potential evaporation which leads to a reduced potential evaporation remaining for the following processes of transpiration and evaporation.

Soil moisture calculation

The water balance equation for the soil layer is solved by using a stepwise linear approach for the processes effecting soil moisture, which are Infiltration, Evaporation, Transpiration, Percolation, Interflow and Capillary-Rise. The input value for evaporation and transpiration is determined through the reduced potential evaporation due to interception evaporation.

The equation to be solved is as follows:

[math]\displaystyle{ \frac{d\theta(t)}{d\mbox{t}} = \mbox{Inf}(t) - \mbox{Perk}(t) - \mbox{Eva}_{akt}(t) - \mbox{Trans}_{akt}(t) - \mbox{Int}(t) + \mbox{Kap}(t) }[/math]

with:

θ(t) = current soil moisture

Inf(t) = infiltration into the soil

Perk(t) = percolation

Evaakt(t) = actual evaporation

Transakt(t) = actual transpiration

Int(t) = interflow

Kap(t) = capillary-rise

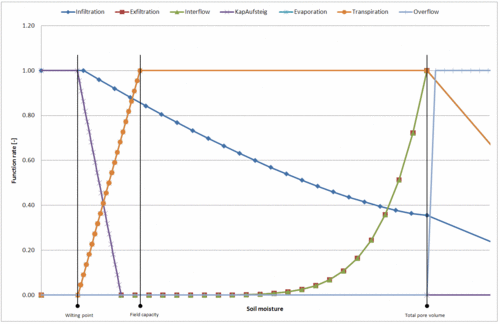
Infiltration, Percolation, Evaporation, Transpiration, Interflow and Capillary-Rise are dependent on the current soil moisture. In the simulation this dependency is described by the following function curves.

Abbildung 40: Depiction of selected soil process functions

with:

kf = saturated hydraulic conductivity

nFK = available water capacity (nFK = FK - WP)

WP = wilting point

FK = field capacity

GPV = total pore volume

I = gradient [-]

fPK = soil specific scaling factor for the percolation function

fEva = soil specific scaling factor for the evaporation function

fTP = soil specific scaling factor for the transpiration function

f1,Int = soil specific scaling factor for the interflow function

f2,Int = soil specific scaling factor for the interflow function

nInt = soil specific scaling factor for the interflow function

nTP = Krümmungsparameter der Transpirationsfunktion

Program parameters are calculated internally. The user only needs to supply the characteristic soil parameters kf, WP, FK and GPV.

The simulation takes place with a newly developed Building-Block for the simulation of reservoirs, whichs process function are to be mapped through a stepwise linear approach.

Infiltration

Infiltration function in BlueM in comparison to the function according to Holtan for a sand-soil

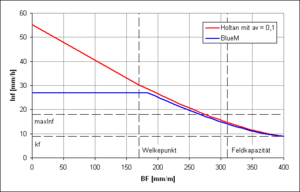
The original approach according to Holtan (1961):

[math]\displaystyle{ \mbox{Inf}(\theta(t)) = \mbox{a}_v \cdot \left ( \mbox{GPV} - \theta(t) \right )^{1,4} + k_f }[/math]

with

av = Vegetation parameter (between 0,1 and 1,0)

is used in a modified form in BlueM:

[math]\displaystyle{ \mbox{Inf}(\theta(t)) = \begin{cases} \mbox{MaxInf} + k_f, & 0 \lt \theta(t) \lt 0,1 \cdot \mbox{nFK} \\ \mbox{MaxInf} \cdot \left( \frac{\mbox{GPV} - \theta(t)}{\mbox{GPV} - 0,1 \cdot \mbox{nFK}} \right) ^{1,4} + k_f, & \theta(t) \ge 0,1 \cdot \mbox{nFK} \end{cases} }[/math]

it needs to be noted that this function only describes the potential Infiltration. Actual Infiltration is limited to the available amount of rain. The modification is a results of the consideration that if it rains on a very dry soil the air within the soil cannot escape and thereby limits maximum infiltration. This leads to a stop of exponential increase in contrast to the original approach of Holtan. ("Flowerpot effect")

Percolation

[math]\displaystyle{ \mbox{Perk}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \\ k_f \cdot \left ( \frac{\theta(t) - \left ( \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \right )}{\mbox{GPV} - \left ( \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \right )} \right )^{n_{PK}}, & \theta(t) \gt \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \end{cases} }[/math]

mod. approach according to Ostrowski (1992), Bear (1988)

→ zu modifizieren in Ansatz nach van Genuchten

Interflow

Interflow is realtivly independent of soil parameters and depends on soil moisture and slope of the individual HRU. (refer to Bug 28):

[math]\displaystyle{ \mbox{Int}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{1,Int} \cdot \mbox{nFK} \\ \theta(t)^{\mbox{n}_{Int}} \cdot \frac{I}{\sqrt{1+I^2}}, & \mbox{f}_{1,Int} \cdot \mbox{nFK} \lt \theta(t) \le \mbox{f}_{2,Int} \cdot \mbox{nFK} \\ \mbox{f}_{2,Int} \cdot \mbox{nFK}, & \theta(t) \gt \mbox{f}_{2,Int} \cdot \mbox{nFK} \end{cases} }[/math]

Evaporation

For the evaporation out of the soil the determined potential evaporation, which was adjusted to land use, is converted into evaporation for fallow land.

[math]\displaystyle{ \mbox{Eva}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{WP} \\ \mbox{f}_{Eva} \cdot \left ( \frac{\theta(t)-\mbox{WP}}{\mbox{GPV}-\mbox{WP}} \right ), & \theta(t) \gt \mbox{WP} \end{cases} }[/math]

Transpiration

[math]\displaystyle{ \mbox{Trans}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP} \\ \mbox{f}_{TP} \cdot \left ( \frac{\theta(t) - \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP}}{\mbox{GPV} - \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP}} \right )^{n_{TP}}, & \theta(t) \gt \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP} \end{cases} }[/math]