Transport elements: Difference between revisions
mNo edit summary |
m (layout) |
||
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{BlueM.Sim_nav}} | ||
{{BlueMTheory_nav}} | |||
__TOC__ | __TOC__ | ||
Transport elements model the translation and retention characteristics of natural streams and rivers or pipes. The calculation approaches of natural channels and pipes differ. | |||
= | [[Bild:Theorie_Abb45.gif|thumb|600px|left|Abbildung 45: Calculations options for the transport element]] | ||
<br clear="left"/> | |||
==Translation== | |||
The wave of inflow reaches the outflow with a certain time offset. This time offset corresponds to the travel time within the transport element. If travel time is shorter than the chosen calculation time step, translation characteristics will not be visible in the simulation results. | |||
==Open conduit calculated using Kalinin-Miljukov== | |||
A wave output is calculated for pipes using Kalinin-Miljikov. The necessary parameters for the Kalinin-Miljukov-Method are estimated program internally according to {{:Literatur:Euler_1983}} for circular pipes. For non circular profiles the parameters are determined by supplying the hydraulic diameter and the cross-section area when the considered profile is completely filled. | |||
:{| cellspacing="0" cellpadding="2" border="0" | :{| cellspacing="0" cellpadding="2" border="0" | ||
|- | |- | ||
| | |characteristic length: || <math>L = 0.4 \cdot \frac{D}{I_S} \quad [\mbox{m}]</math> | ||
|- | |- | ||
| | |retention constant: || <math>K = 0.64 \cdot L \cdot \frac{D^2}{Q_v} \quad [\mbox{s}]</math> | ||
|} | |} | ||
: | :with: | ||
:<code>D</code> [m] = | :<code>D</code> [m] = diameter of the circular pipe respectively hydraulic diameter | ||
:<code>I<sub>S</sub></code> [-] = | :<code>I<sub>S</sub></code> [-] = bottom slope of the pipe | ||
:<code>Q<sub>v</sub></code> [m³/s] = | :<code>Q<sub>v</sub></code> [m³/s] = maximum discharge capacity of the pipe | ||
Maximum discharge capacity is calculated using the Prandtl-Colebrook equation: | |||
:<math>Q_v = A_v \left [ -2 \cdot \lg \left [ \frac{2.51 \cdot \nu}{D\sqrt{2gDI_S}}+\frac{k_b}{3.71 \cdot b} \right ] \cdot \sqrt{2gDI_S} \right ]</math> | :<math>Q_v = A_v \left [ -2 \cdot \lg \left [ \frac{2.51 \cdot \nu}{D\sqrt{2gDI_S}}+\frac{k_b}{3.71 \cdot b} \right ] \cdot \sqrt{2gDI_S} \right ]</math> | ||
: | :with: | ||
:<code>A<sub>v</sub></code> [m²] = | :<code>A<sub>v</sub></code> [m²] = cross-section area of the profile | ||
:<code>ν</code> [m²/s] = | :<code>ν</code> [m²/s] = kinematic viscosity | ||
:<code>k<sub>b</sub></code> [m] = | :<code>k<sub>b</sub></code> [m] = roughness | ||
:<code>g</code> [m/s²] = | :<code>g</code> [m/s²] = gravitational acceleration | ||
:<math>n = \frac{L_g}{L}</math> ( | Corresponding to the characteristic length <code>L</code> the total length <code>L<sub>g</sub></code> of the element is split into <code>n</code> calculation segments of equal length. | ||
:with: | |||
:<math>n = \frac{L_g}{L}</math> (in which n is an integer) | |||
The adjusted parameters are valid for the individual calculation segments. | |||
:<math>L^* = \frac{L_g}{n}</math> | :<math>L^* = \frac{L_g}{n}</math> | ||
:<math>K^* = K \cdot \frac{L^*}{L}</math> | :<math>K^* = K \cdot \frac{L^*}{L}</math> | ||
On the basis of these parameters the outflow at the downstream end of the element is calculated by running through the recursion formula <code>n</code> times. | |||
:recursion formula: | |||
:<math>Q_{a,i} = Q_{a,i-1} + C_1 \cdot (Q_{z,i-1} - Q_{a,i-1}) + C_2 \cdot (Q_{z,i} - Q_{z,i-1})</math> | :<math>Q_{a,i} = Q_{a,i-1} + C_1 \cdot (Q_{z,i-1} - Q_{a,i-1}) + C_2 \cdot (Q_{z,i} - Q_{z,i-1})</math> | ||
: | :with | ||
:<code>Q<sub>z</sub></code> = | :<code>Q<sub>z</sub></code> = Inflow to the calculation segment | ||
:<code>Q<sub>a</sub></code> = | :<code>Q<sub>a</sub></code> = Outflow of the calculation segment | ||
:<code>i</code> = | :<code>i</code> = current calculation time step | ||
:<code>i-1</code> = | :<code>i-1</code> = antecedent calculation time step | ||
:<code>dt</code> = | :<code>dt</code> = time step increment | ||
:<math>C_1 = 1 - e^{-\frac{dt}{K^*}}</math> | :<math>C_1 = 1 - e^{-\frac{dt}{K^*}}</math> | ||
:<math>C_2 = 1 - \frac{\frac{K^*}{dt}}{C_1}</math> | :<math>C_2 = 1 - \frac{\frac{K^*}{dt}}{C_1}</math> | ||
This approximation approach derived by Kalinin-Miljukov is a reservoir cascade as utilized for run-off concentration. Therefore the wave output of a transport element can be simulated through a reservoir cascade of <code>n</code> reservoirs with the retention constant <code>K*</code>. | |||
This method was validated according to the paper of {{:Literatur:Euler_1983}} (refer to {{file|pdf|Test_KalMil.pdf|Test_KalMil.pdf}}). | |||
== | ==Open Channel flow with input of channel geometry== | ||
[[Bild:CharLaenge.gif|thumb|300px]] | [[Bild:CharLaenge.gif|thumb|300px]] | ||
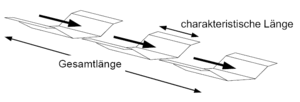
Translation and retention characteristics are modeled for open channel flow by using Kalinin-Miljukov as well. The characteristic length as a Parameter of the Kalinin-Miljukov-Method is derived out of the uniform flow relationship according to Manning-Strickler ({{:Literatur:Rosemann_1970}}). | |||
Via the characteristic length the channel is split into individual segments. For each segment transmission behavior is modeled with a non-linear reservoir (refer to [[Speicherbaustein]])with help of the uniform flow relationship. | |||
;Hint : For the simulation in BlueM a fictional vertical wall of 1m height is added to the provided channel geometry/profile in the [[TRS-File]].<br clear="all" /> | |||
==Using a water level – cross-section area - discharge characteristic curve== | |||
If the transmission behavior of a transport element is known through prior water level calculation, the results can be used in the form of a water level- cross-section area- discharge characteristic curve. | |||
==Open conduit pipes using a non-linear reservoir== | |||
The calculation utilizes the building block (a non-linear [[Speicherbaustein|reservoir]])according to {{:Literatur:Ostrowski_1992}}. | |||
The wave outflow is calculated via Teilfüllungs- bzw. Teilabflusskurve. Thereby the non-linear component of the outflow process is considered as opposed to the calculation using Kalinin-Miljukov. | |||
== | ==Literature== | ||
<references/> | <references/> | ||
[[Kategorie:BlueM Theorie]] | |||
[[Kategorie: | |||
Latest revision as of 07:31, 9 January 2015
![]() BlueM.Sim | Download | Application | Theory | Development
BlueM.Sim | Download | Application | Theory | Development
BlueM.Sim theory
Transport elements model the translation and retention characteristics of natural streams and rivers or pipes. The calculation approaches of natural channels and pipes differ.
Translation
The wave of inflow reaches the outflow with a certain time offset. This time offset corresponds to the travel time within the transport element. If travel time is shorter than the chosen calculation time step, translation characteristics will not be visible in the simulation results.
Open conduit calculated using Kalinin-Miljukov
A wave output is calculated for pipes using Kalinin-Miljikov. The necessary parameters for the Kalinin-Miljukov-Method are estimated program internally according to Euler (1983)[1] for circular pipes. For non circular profiles the parameters are determined by supplying the hydraulic diameter and the cross-section area when the considered profile is completely filled.
characteristic length: [math]\displaystyle{ L = 0.4 \cdot \frac{D}{I_S} \quad [\mbox{m}] }[/math] retention constant: [math]\displaystyle{ K = 0.64 \cdot L \cdot \frac{D^2}{Q_v} \quad [\mbox{s}] }[/math]
- with:
D[m] = diameter of the circular pipe respectively hydraulic diameterIS[-] = bottom slope of the pipeQv[m³/s] = maximum discharge capacity of the pipe
Maximum discharge capacity is calculated using the Prandtl-Colebrook equation:
- [math]\displaystyle{ Q_v = A_v \left [ -2 \cdot \lg \left [ \frac{2.51 \cdot \nu}{D\sqrt{2gDI_S}}+\frac{k_b}{3.71 \cdot b} \right ] \cdot \sqrt{2gDI_S} \right ] }[/math]
- with:
Av[m²] = cross-section area of the profileν[m²/s] = kinematic viscositykb[m] = roughnessg[m/s²] = gravitational acceleration
Corresponding to the characteristic length L the total length Lg of the element is split into n calculation segments of equal length.
- with:
- [math]\displaystyle{ n = \frac{L_g}{L} }[/math] (in which n is an integer)
The adjusted parameters are valid for the individual calculation segments.
- [math]\displaystyle{ L^* = \frac{L_g}{n} }[/math]
- [math]\displaystyle{ K^* = K \cdot \frac{L^*}{L} }[/math]
On the basis of these parameters the outflow at the downstream end of the element is calculated by running through the recursion formula n times.
- recursion formula:
- [math]\displaystyle{ Q_{a,i} = Q_{a,i-1} + C_1 \cdot (Q_{z,i-1} - Q_{a,i-1}) + C_2 \cdot (Q_{z,i} - Q_{z,i-1}) }[/math]
- with
Qz= Inflow to the calculation segmentQa= Outflow of the calculation segmenti= current calculation time stepi-1= antecedent calculation time stepdt= time step increment- [math]\displaystyle{ C_1 = 1 - e^{-\frac{dt}{K^*}} }[/math]
- [math]\displaystyle{ C_2 = 1 - \frac{\frac{K^*}{dt}}{C_1} }[/math]
This approximation approach derived by Kalinin-Miljukov is a reservoir cascade as utilized for run-off concentration. Therefore the wave output of a transport element can be simulated through a reservoir cascade of n reservoirs with the retention constant K*.
This method was validated according to the paper of Euler (1983)[1] (refer to Test_KalMil.pdf ![]() ).
).
Open Channel flow with input of channel geometry
Translation and retention characteristics are modeled for open channel flow by using Kalinin-Miljukov as well. The characteristic length as a Parameter of the Kalinin-Miljukov-Method is derived out of the uniform flow relationship according to Manning-Strickler (Rosemann (1970)[2]).
Via the characteristic length the channel is split into individual segments. For each segment transmission behavior is modeled with a non-linear reservoir (refer to Speicherbaustein)with help of the uniform flow relationship.
- Hint
- For the simulation in BlueM a fictional vertical wall of 1m height is added to the provided channel geometry/profile in the TRS-File.
Using a water level – cross-section area - discharge characteristic curve
If the transmission behavior of a transport element is known through prior water level calculation, the results can be used in the form of a water level- cross-section area- discharge characteristic curve.
Open conduit pipes using a non-linear reservoir
The calculation utilizes the building block (a non-linear reservoir)according to Ostrowski (1992)[3]. The wave outflow is calculated via Teilfüllungs- bzw. Teilabflusskurve. Thereby the non-linear component of the outflow process is considered as opposed to the calculation using Kalinin-Miljukov.
Literature
- ↑ 1.0 1.1 Euler, G. (1983): Ein hydrologisches Näherungsverfahren für die Berechnung des Wellenablaufs in Kreisrohren. Wasser und Boden (Heft 2) (PDF
 )
)
- ↑ Rosemann, H.-J., Vedral, J. (1970): Das Kalinin-Miljukov Verfahren zur Berechnung des Ablaufs von Hochwasserwellen. Schriftenreihe der bayerischen Landesstelle für Gewässerkunde München, Heft 6
- ↑ Ostrowski, M. (1992): Ein universeller Baustein zur Simulation hydrologischer Prozesse, Wasser und Boden, Heft 11 (PDF
 )
)