Rural Catchments

{{#hierarchy-top:}}

The natural process leading from rain to run-off is divided into three phases. The phases are Belastungsbildung, run-off generation (bzw. Belastungsaufteilung) and run-off concentration. The calculation approach for each of these phases is described in the following sections of this article.

Belastungsbildung

Die Belastungsbildung describes the determination of an areal rainfall for the considered catchment.Rainfall data is imported into BlueM via external time series. Therefore no explicit calculations are necessary for this phase.

Run-off generation

In this phase surface run-off, infiltration, evaporation and interflow are determined by calculating the effective rainfall out of the fallen rain. Snow is calculated for temperatures below 0°C. The Snow-Compaction-Method Knauf is applied.

Rainfall (system load) is divided into rainfall which directly generates run-off and run-off diminishing losses (wetting, trough, evaporation and infiltration losses). Therefore this phase is also called the Belastungsaufteilung. The mathematical equation for the momentary Belastungsaufteilung is as follows:

[math]\displaystyle{ Nw(t) = N(t) - VP(t) - I(t) - \frac{dO}{dt} - \frac{dS}{dt} }[/math]

mit:

NW = run-off generating rainfall

N = rainfall

VP = potential evaporation

I = infiltration into the soil

O = surfacce water reservoir content

S = snow reservoir content

The individual elements of the equation and the calculation the calculation of these elements is described in the following.

Niederschlag N(t)

Die Niederschlagsdaten müssen dem Simulationsmodell in Form von Regenreihen zur Verfügung gestellt werden. Hierbei ist es prinzipiell unerheblich, ob die Niederschlagsreihe ein Blockregen, ein Modellregen, ein gemessener natürlicher Regen, ein Regenspektrum oder eine langjährige Regenreihe ist. Je nach Zielsetzung der Simulationsrechnung ist die geeignete Belastung ausgewählt werden. Die Regenreihen stammen entweder aus der Zeitreihenverwaltung von BlueM oder werden wie bei Anwendung einer Kurzfristprognose durch die Eingabe einer Regendauer, einer Niederschlagshöhe und der Wahl eines Modellregens direkt vor einer Simulation erzeugt.

Verdunstung VP(t)

Es bestehen zwei Optionen für die Eingabe einer potentiellen Verdunstung:

a) Jahresverdunstungssumme

Abbildung 33: Jahresgang der potentiellen Verdunstung nach Brandt (1979)

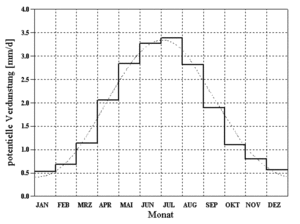
Es wird ein normierter Jahresgang der potentiellen Verdunstung nach Brandt für die Berechnung der potentiellen Verdunstung herangezogen. Aus ausgewerteten Messungen von 20 Stationen, deren Mittelwerte als Histogramm in Abbildung 33 dargestellt sind, wurde folgende Ausgleichsfunktion (gepunktete Linie in Abbildung 33) ermittelt:

[math]\displaystyle{ VP[\mbox{mm/d}] = \begin{cases}(0.96 + 0.0033 \cdot i) \cdot \sin(\frac{2 \pi}{365})(i - 148) + 1.58, & i \lt = 300 \\ 2.56 - 1.53 / 65. \cdot (i - 300.), & i \gt 300 \end{cases} }[/math]

mit

i = laufender Tag des hydrologischen Jahres

i = 1 → 1. November

Die potentielle Verdunstung nach Brandt bezieht sich auf die Grasreferenzverdunstung und geht von einer Jahresverdunstungshöhe von 654,282 mm aus. Wird eine abweichende Jahresverdunstungshöhe eingegeben, wird der nach Brandt ermittelte Wert entsprechend skaliert.

b) Verdunstungszeitreihe

Ist eine Verdunstungszeitreihe gegeben, wird der entsprechende Wert des Zeitschrittes eingelesen.
Vorsicht: Bei einem Simulationszeitschritt < 1d wird der Zeitreihenwert zusätzlich mit einem Tagesgang überprägt! (Bug 1)

Verdunstungstagesgang

Abbildung 34: Tagesgang der potentiellen Verdunstung als Vielfaches der mittleren Tagesverdunstung

Ist das gewählte Berechnungszeitintervall kleiner als ein Tag, wird mittels dem in Abbildung 34 dargestellten Tagesgang die potentielle Verdunstung für jedes Berechnungszeitintervall ermittelt. Ist das Berechnungsintervall ≥ 1 Tag entfällt die Berücksichtigung des Tagesganges.

Oberflächenwasservorrat (Versiegelter Flächenanteil) O

Bei den versiegelten Flächenanteilen kann neben dem Schneevorrat auch die Infiltration vernachlässigt werden, so dass sich die Bilanzgleichung wie folgt vereinfacht:

[math]\displaystyle{ Nw(t) = N(t) - VP(t) - \frac{dO}{dt} }[/math]

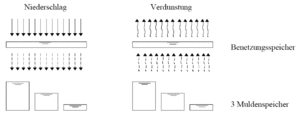
wobei die Oberflächenwasservorratsänderung dO/dt die Benetzung der Oberfläche sowie die Auffüllung und Entleerung (durch Verdunstung) der Mulden repräsentiert.

Als Benetzungsverlust BV für versiegelte Flächen wird folgender Standardwert angesetzt.

BV = 0.5 mm

Der Muldenverlust MV wird durch den Anwender vorgegeben.

Der Muldenverlust stellt den Mittelwert für eine geneigte Oberfläche dar. Da die Mulden jedoch nicht gleichmäßig verteilt sind und erfahrungsgemäß bereits ein Abfluss einsetzt, bevor überall die komplette Muldenauffüllung erreicht ist, wird unterstellt, dass jeweils

Abbildung 35: Schema der Modellansätze Benetzungs- und Muldenverluste

• 1/3 der versiegelten Fläche einen verminderten Muldenverlust von 1/3 MV
• 1/3 der versiegelten Fläche den mittleren Muldenverlust von 3/3 MV
• 1/3 der versiegelten Fläche einen erhöhten Muldenverlust von 5/3 MV

aufweist. Somit kommt es bereits zum Abfluss, wenn der um die Verdunstungsrate verminderte Niederschlag den Benetzungsverlust und 1/3 des Muldenverlustes übersteigt (bei trockener Vorgeschichte). In Abbildung 35 sind die o.g. Annahmen schematisch skizziert.

Der Abflussbeiwert der versiegelten Flächen (nach Abdeckung der Anfangsverluste) wird mit ψ = 1 angesetzt. Bei der Festlegung des versiegelten Flächenanteils in einem Teileinzugsgebiet ist zu beachten, dass nicht alle befestigten oder versiegelten Flächen tatsächlich in eine Kanalisation entwässern.

Die kontinuierliche Bereitstellung der Benetzungs- und Muldenverluste erfolgt über die laufende Bilanzierung dieser Speicher und der Verdunstung.

Oberflächenwasservorrat (unversiegelter Flächenanteil) O

Der Oberflächenwasservorrat wird über die Bilanzierung eines Verlustspeichers in Abhängigkeit des gewählten Abflussbildungsansatzes berechnet. Einzelheiten dazu finden sich in den folgenden Abschnitten zur Berechnung der Infiltration bzw. abflusswirksamer Niederschlag.

Infiltration bzw. abflusswirksamer Niederschlag I(t), Nw(t)

Bei den durchlässigen Flächen kann die Infiltration in den Boden nicht vernachlässigt werden, da diese das Abflussgeschehen entscheidend prägt. Für die Berechnung wurden drei Ansätze im Modell implementiert:

1. Konstanter Abflussbeiwert ψ
2. Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)
3. Bodenfeuchtesimulation

Konstanter Abflussbeiwert ψ

Bei Angabe eines ψ_u-Wertes kommt nach Abdeckung der Anfangsverluste (Benetzungs- und Muldenverlust) der übrige Anteil des Niederschlages im Verhältnis des Abflussbeiwertes ψ_u zum Abfluss und zwar unabhängig von der Vorgeschichte und den Merkmalen des Niederschlages (Höhe, Intensität, Dauer). Auf diesen Ansatz sollte nach Möglichkeit verzichtet werden, da hier der Prozess der Abflussbildung nur grob vereinfachend beschrieben wird.

SCS-Verfahren

siehe SCS-Verfahren

Bodenfeuchtesimulation

siehe Bodenfeuchtesimulation

Abflusskonzentration

Abbildung 44: Berechnung der Abflusskonzentration von natürlichen Einzugsgebieten

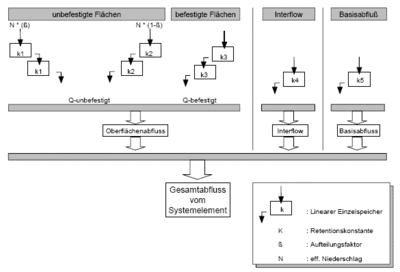
Die Abflusskonzentration bestimmt die Verzögerung des Abflusses aus dem Einzugsgebiet. Die Berechnung von Interflow und Basisabfluss ist abhängig vom Berechnungsansatz. Bei der Berechungsoption Bodenfeuchteberechnung werden die beiden Abflusskomponenten über einen linearen Einzelspeicher verzögert an den Elementausgang abgegeben. Bei den Berechungsoptionen Abflussbeiwert und SCS-Verfahren wird kein Interflow berücksichtigt und der Basisabfluss entsprechend der angegebenen Basisabflussspende unter möglicher Berücksichtigung eines Jahresgangs ermittelt.

Es wird eine Parallelspeicherkaskade mit jeweils zwei Speichern für unbefestigte und eine Kaskade mit ebenfalls zwei Speichern für befestigte Flächen benutzt. Die Speicherkaskaden können entweder als Linearspeicher oder als nichtlineare Speicher berechnet werden. Werden die Parameter für die Speicherkaskade nicht vorgegeben, erfolgt die Berchenung an Hand der Gebietskenngrößen gemäß Zaiß (1986).

Literaturangaben

{{#hierarchy-bottom:}}