Urban Catchments

{{#hierarchy-top:}}

Analog to rural catchments the natural process leading from rain to run-off is divided into three phases for urban catchments. The phases are Belastungsbildung, run-off generation (bzw. Belastungsaufteilung) and run-off concentration. The calculation approach for each of these phases is described in the following sections of this article.

Belastungsbildung

Die Belastungsbildung describes the determination of an areal rainfall for the considered catchment.Rainfall data is imported into BlueM via external time series. Therefore no explicit calculations are necessary for this phase.

Run-off Generation

The run-off generation phase determines the amount of rain out of the amount of fallen rain which leads to run-off generation. Rainfall (system load) is divided into rainfall which directly generates run-off and run-off diminishing losses (wetting, trough, evaporation and infiltration losses). Therefore this phase is also called the Belastungsaufteilung. Snowfall is neglected in urban catchments.

In General pervious and impervious areas are calculated separately. Impervious area is calculated through the total area and the fraction of impervious area:

[math]\displaystyle{ A_{bef} = VG \cdot A_{ges} }[/math]

impervious areas

Effective rainfall for impervious areas is calculated by balancing rainfall, evaporation and the surface reservoir. The surface reservoir is made up of troughs and wetting areas. Troughs and wetting areas are described in more detail in the section "surface water reservoir content". The following equation is derived:

[math]\displaystyle{ Nw(t) = N(t) - VP(t) - \frac{dO}{dt} }[/math]

with:

NW = run-off generating rainfall

N = rainfall

VP = potential evaporation

O = surface water reservoir content

The run-off coefficient of impervious areas is generally set to ψ = 1. Therefore all remaining water - after having covered initial losses - contributes to surface run-off. It needs to be noted that not all impervious areas drain into the canalization. Typically about 10-20% of impervious areas do not drain into the canalization.

pervious areas

For pervious areas the run-off coefficient is ψ <= 1. This is due to the fact, that not all remaining water -after having covered initial losses - contributes to surface run-off on pervious areas. Infiltration is taken into consideration by applying a run-off coefficient <1. ψ can be supplied by the user or can be calculated via the SCS-Method. The equation for momentary load distribution is as follows:

[math]\displaystyle{ Nw(t) = N(t) - VP(t) - I(t) - \frac{dO}{dt} }[/math]

with:

NW = run-off generating rainfall abflusswirksamer

N = rainfall

VP = potential evaporation

I = infiltration into the soil

O = surface water reservoir content

In the following segments the losses are described in further detail:

Evaporation

There are two possibilities for the input of potential evaporation. Both options calculate a daily evaporation value. If the chosen time step for the calculation is < 1 day the potential evaporation for each time step is calculated by taking the daily pattern depicted in Abbildung 34 into consideration. If the chosen time step is ≥ 1 day the daily pattern is disregarded.

Abbildung 34: Daily pattern of potential evaporation as a multiple of mean daily evaporation

a) annual evaporation

Abbildung 33: annual pattern of potential evaporation according to Brandt (1979)

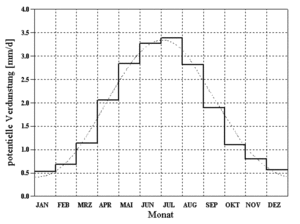
A normed annual pattern of potential evaporation according to Brandt is utilized for the calculation of potential evaporation. Through the evaluation of measurements from twenty different stations, whichs mean-values are depicted as a histogram in Abbildung 33, the following smoothing function was derived (doted line in Abbildung 33):

[math]\displaystyle{ VP[\mbox{mm/d}] = \begin{cases}(0.96 + 0.0033 \cdot i) \cdot \sin(\frac{2 \pi}{365})(i - 148) + 1.58, & i \lt = 300 \\ 2.56 - 1.53 / 65. \cdot (i - 300.), & i \gt 300 \end{cases} }[/math]

with

i = ongoing day of the hydrological year

i = 1 → 1. November

Potential evaporation according to Brandt refers to grass reference evaporation and assumes an annual total evaporation loss of 654,282 mm. If a different annual total evaporation loss is entered, the value determined by Brandt is scaled accordingly.

b) evaporation time series

If a evaporation time series is supplied the utilized time step is imported.
Attention: For time steps < 1 day the time series value is additionally overprinted with a daily pattern! (Bug 1)

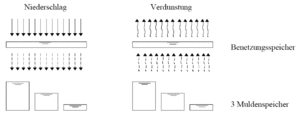
Oberflächenwasservorrat

Befestigte Flächenanteile

Die Oberflächenwasservorratsänderung dO/dt repräsentiert die Benetzung der Oberfläche sowie die Auffüllung und Entleerung (durch Verdunstung) der Mulden.

Als Benetzungsverlust BV für versiegelte Flächen wird folgender Standardwert angesetzt.

BV = 0.5 mm

Der Muldenverlust MV wird durch den Anwender vorgegeben.

Der Muldenverlust stellt den Mittelwert für eine geneigte Oberfläche dar. Da die Mulden jedoch nicht gleichmäßig verteilt sind und erfahrungsgemäß bereits ein Abfluss einsetzt, bevor überall die komplette Muldenauffüllung erreicht ist, wird unterstellt, dass jeweils

Abbildung 35: Schema der Modellansätze Benetzungs- und Muldenverluste

• 1/3 der versiegelten Fläche einen verminderten Muldenverlust von 1/3 MV
• 1/3 der versiegelten Fläche den mittleren Muldenverlust von 3/3 MV
• 1/3 der versiegelten Fläche einen erhöhten Muldenverlust von 5/3 MV

aufweist. Somit kommt es bereits zum Abfluss, wenn der um die Verdunstungsrate verminderte Niederschlag den Benetzungsverlust und 1/3 des Muldenverlustes übersteigt (bei trockener Vorgeschichte). In Abbildung 35 sind die o.g. Annahmen schematisch skizziert.

Die kontinuierliche Bereitstellung der Benetzungs- und Muldenverluste erfolgt über die laufende Bilanzierung dieser Speicher und der Verdunstung.

Unbefestigte Flächenanteile

Der Oberflächenwasservorrat wird über die Bilanzierung eines Verlustspeichers in Abhängigkeit des gewählten Abflussbildungsansatzes berechnet. Einzelheiten dazu finden sich in den folgenden Abschnitten zur Berechnung der Infiltration.

Infiltration

Bei den unbefestigten Flächenanteilen kann die Infiltration in den Boden nicht vernachlässigt werden, da diese das Abflussgeschehen entscheidend prägt. Für die Berechnung wurden zwei Ansätze im Modell implementiert:

1. Konstanter Abflussbeiwert ψ
2. Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)

Konstanter Abflussbeiwert ψ

Bei Angabe eines ψ_u-Wertes kommt nach Abdeckung der Anfangsverluste (Muldenverlust sowie Verdusntung) der übrige Anteil des Niederschlages im Verhältnis des Abflussbeiwertes ψ_u zum Abfluss und zwar unabhängig von der Vorgeschichte und den Merkmalen des Niederschlages (Höhe, Intensität, Dauer).

Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)

Bei Angabe eines vom Bodentyp und der Bodennutzung abhängigen CN-Wertes (siehe DVWK (1991)) lässt sich ein vorgeschichtsabhängiger Anfangsverlust sowie eine vorgeschichtsabhängige Beziehung des Abflussbeiwertes von der bis zum betrachteten Zeitpunkt akkumulierten Niederschlagshöhe formulieren (cp. Zaiß (1989)); d.h. der Abflussbeiwert wächst mit zunehmendem Niederschlag im Verlauf des Ereignisses an.

Die Quantifizierung der Vorgeschichte erfolgt über den 21-Tage-Vorregenindex VN

[math]\displaystyle{ V_N = \sum_{j=1}^{21} C(j)^j \cdot h_{N,j} }[/math]

mit

hN,j = Niederschlagshöhe des j-ten Vortags

C(j) = Faktor, der den Einfluss des j-ten Vortags beschreibt

Der Einfluss der Jahreszeit wird durch einen Jahresgang des Faktors C wiedergegeben.

[math]\displaystyle{ C = 0.05 \cdot \sin\left(\frac{2 \pi}{365}\right) (i + 0.75 ) + 0.85 }[/math]

mit

i = lfd. Tag des Abflussjahres

Abbildung 36: Abhängigkeit des Abflussbeiwertes von der Vorgeschichte

Damit schwankt der Wert C zwischen 0,8 < C < 0,9. Hierdurch wird erreicht, dass bei gleichem Vorregen zu unterschiedlichen Jahreszeiten unterschiedliche Vorregenindizes berechnet und damit eine veränderte Abflussbereitschaft in Rechnung gestellt wird.

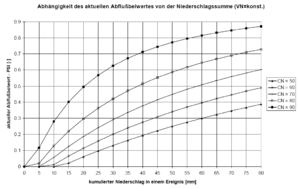
In Abhängigkeit von der auf diese Weise quantifizierten Vorgeschichte kann unter Verwendung der gebietsspezifischen und für mittlere Vorfeuchteverhältnisse gültigen CN-Werte ein aktueller Abflussbeiwert berechnet werden. In Abbildung 36 ist für unterschiedliche CN-Werte dargestellt, wie sich der aktuelle Abflussbeiwert in Abhängigkeit von der Vorgeschichte verändert.

Abbildung 37: Abhängigkeit des Abflussbeiwertes von der kumulierten Niederschlagssumme

Da sich im Verlaufe eines Regenereignisses durch die Durchfeuchtung des Bodens die Abflussbereitschaft eines Einzugsgebiets verändert, wird ebenfalls eine Anpassung des Abflussbeiwertes während eines Ereignisses als Funktion der kumulierten Niederschlagshöhe vorgenommen. In Abbildung 37 ist dieser Zusammenhang für unterschiedliche CN-Werte dargestellt.

Abflusskonzentration

Die Abflusskonzentration bestimmt die Verzögerung des Oberflächenabflusses aus dem Einzugsgebiet. Interflow und Basisabfluss werden bei urbanen Einzugsgebieten nicht berücksichtigt, da die kanalisierten Flächen als Teil des Entwässerungssystems ausschließlcih Oberflächenwasser in der Kanalisation weiterleiten.

Die Berechnung des Oberflächenabflusses erfolgt mit Hilfe einer Parallelspeicherkaskade mit jeweils drei Speichern. Der abflusswirksame Niederschlag des Gesamtgebiets wird durch Mittelwertbildung über die befestigten und unbefestigten Flächen berechnet. Die Aufteilung auf die beiden Speicherkaskaden erfolgt an Hand der Größe des Einzugsgebiets, die Retentionskonstanten der Speicher an Hand der Fließzeit im Einzugsgebiet (siehe Ostrowski et al. (1998)).

Literaturangaben

{{#hierarchy-bottom:}}