Transport elements: Difference between revisions
(Start Translation) |
mNo edit summary |
||
| Line 24: | Line 24: | ||
|} | |} | ||
:with | :with: | ||
:<code>D</code> [m] = diameter of the circular pipe respectively hydraulic diameter | :<code>D</code> [m] = diameter of the circular pipe respectively hydraulic diameter | ||
:<code>I<sub>S</sub></code> [-] = bottom slope of the pipe | :<code>I<sub>S</sub></code> [-] = bottom slope of the pipe | ||
| Line 39: | Line 39: | ||
:<code>g</code> [m/s²] = gravitational acceleration | :<code>g</code> [m/s²] = gravitational acceleration | ||
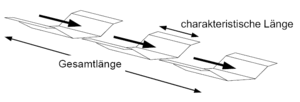
Corresponding to the characteristic length <code>L</code> the total length <code>L<sub>g</sub></code> of the element is split into <code>n</code> calculation segments of equal length. | |||
:<math>n = \frac{L_g}{L}</math> ( | :with: | ||
:<math>n = \frac{L_g}{L}</math> (in which n is an integer) | |||
The adjusted parameters are valid for the individual calculation segments. | |||
:<math>L^* = \frac{L_g}{n}</math> | :<math>L^* = \frac{L_g}{n}</math> | ||
:<math>K^* = K \cdot \frac{L^*}{L}</math> | :<math>K^* = K \cdot \frac{L^*}{L}</math> | ||
On the basis of these parameters the outflow at the downstream end of the element is calculated by running through the recursion formula <code>n</code> times. | |||
:recursion formula: | |||
:<math>Q_{a,i} = Q_{a,i-1} + C_1 \cdot (Q_{z,i-1} - Q_{a,i-1}) + C_2 \cdot (Q_{z,i} - Q_{z,i-1})</math> | :<math>Q_{a,i} = Q_{a,i-1} + C_1 \cdot (Q_{z,i-1} - Q_{a,i-1}) + C_2 \cdot (Q_{z,i} - Q_{z,i-1})</math> | ||
: | :with | ||
:<code>Q<sub>z</sub></code> = | :<code>Q<sub>z</sub></code> = Inflow to the calculation segment | ||
:<code>Q<sub>a</sub></code> = | :<code>Q<sub>a</sub></code> = Outflow of the calculation segment | ||
:<code>i</code> = aktueller | :<code>i</code> = current calculation time step aktueller | ||
:<code>i-1</code> = | :<code>i-1</code> = antecedent calculation time step | ||
:<code>dt</code> = | :<code>dt</code> = time step increment | ||
:<math>C_1 = 1 - e^{-\frac{dt}{K^*}}</math> | :<math>C_1 = 1 - e^{-\frac{dt}{K^*}}</math> | ||
:<math>C_2 = 1 - \frac{\frac{K^*}{dt}}{C_1}</math> | :<math>C_2 = 1 - \frac{\frac{K^*}{dt}}{C_1}</math> | ||
Dieses von Kalinin-Miljukov abgeleitete Näherungsverfahren ist nichts anderes als die bei der Abflusskonzentration verwendete Speicherkaskade; d.h. der Wellenablauf in einer Transportstrecke lässt sich durch eine Speicherkaskade bestehend aus <code>n</code> Speichern mit der Speicherkonstante <code>K*</code> simulieren. | Dieses von Kalinin-Miljukov abgeleitete Näherungsverfahren ist nichts anderes als die bei der Abflusskonzentration verwendete Speicherkaskade; d.h. der Wellenablauf in einer Transportstrecke lässt sich durch eine Speicherkaskade bestehend aus <code>n</code> Speichern mit der Speicherkonstante <code>K*</code> simulieren. | ||
Revision as of 00:13, 4 June 2013
{{#hierarchy-top:}}
Transport elements model the translation and retention characteristics of natural streams and rivers or pipes. The calculation approaches of natural channels and pipes differ.
Translation
The wave of inflow reaches the outflow with a certain time offset. This time offset corresponds to the travel time within the transport element. If travel time is shorter than the chosen calculation time step, translation characteristics will not be visible in the simulation results.
Open conduit calculated using Kalinin-Miljukov
A wave output is calculated for pipes using Kalinin-Miljikov. The necessary parameters for the Kalinin-Miljukov-Method are estimated program internally according to Euler (1983)[1] for circular pipes. For non circular profiles the parameters are determined by supplying the hydraulic diameter and the cross-section area when the considered profile is completely filled.
characteristic length: [math]\displaystyle{ L = 0.4 \cdot \frac{D}{I_S} \quad [\mbox{m}] }[/math] retention constant: [math]\displaystyle{ K = 0.64 \cdot L \cdot \frac{D^2}{Q_v} \quad [\mbox{s}] }[/math]
- with:
D[m] = diameter of the circular pipe respectively hydraulic diameterIS[-] = bottom slope of the pipeQv[m³/s] = maximum discharge capacity of the pipe
Maximum discharge capacity is calculated using the Prandtl-Colebrook equation:
- [math]\displaystyle{ Q_v = A_v \left [ -2 \cdot \lg \left [ \frac{2.51 \cdot \nu}{D\sqrt{2gDI_S}}+\frac{k_b}{3.71 \cdot b} \right ] \cdot \sqrt{2gDI_S} \right ] }[/math]
- with:
Av[m²] = cross-section area of the profileν[m²/s] = kinematic viscositykb[m] = roughnessg[m/s²] = gravitational acceleration
Corresponding to the characteristic length L the total length Lg of the element is split into n calculation segments of equal length.
- with:
- [math]\displaystyle{ n = \frac{L_g}{L} }[/math] (in which n is an integer)
The adjusted parameters are valid for the individual calculation segments.
- [math]\displaystyle{ L^* = \frac{L_g}{n} }[/math]
- [math]\displaystyle{ K^* = K \cdot \frac{L^*}{L} }[/math]
On the basis of these parameters the outflow at the downstream end of the element is calculated by running through the recursion formula n times.
- recursion formula:
- [math]\displaystyle{ Q_{a,i} = Q_{a,i-1} + C_1 \cdot (Q_{z,i-1} - Q_{a,i-1}) + C_2 \cdot (Q_{z,i} - Q_{z,i-1}) }[/math]
- with
Qz= Inflow to the calculation segmentQa= Outflow of the calculation segmenti= current calculation time step aktuelleri-1= antecedent calculation time stepdt= time step increment- [math]\displaystyle{ C_1 = 1 - e^{-\frac{dt}{K^*}} }[/math]
- [math]\displaystyle{ C_2 = 1 - \frac{\frac{K^*}{dt}}{C_1} }[/math]
Dieses von Kalinin-Miljukov abgeleitete Näherungsverfahren ist nichts anderes als die bei der Abflusskonzentration verwendete Speicherkaskade; d.h. der Wellenablauf in einer Transportstrecke lässt sich durch eine Speicherkaskade bestehend aus n Speichern mit der Speicherkonstante K* simulieren.
Das Verfahren wurde an Hand der Veröffentlichung von Euler (1983)[1] überprüft (siehe Test_KalMil.pdf ![]() ).
).
Offene Gerinne mit Angabe eines Querprofils
Auch hier wird mit Hilfe der Wellenablaufberechnung nach Kalinin-Miljukov das Translations- und Retentionsverhalten abgebildet. Aus der Normalabflussbeziehung nach Manning-Strickler wird die charakteristische Länge als Parameter des Kalinin-Miljukov-Verfahrens abgeleitet (Rosemann (1970)[2]).
Mit der charakteristischen Länge erfolgt für das Gerinne eine Aufteilung in einzelne Segmente. Für jedes Segment wird mit Hilfe der Normalabflussbeziehung über eine nichtlineare Speicherberechnung (siehe Speicherbaustein) die Berechnung des Übertragungsverhaltens vollzogen.
- Hinweis
- Für die Simulation in BlueM wird das in der TRS-Datei eingegebene Profil an beiden Seiten durch eine fiktive senkrechte Wand von 1m Höhe ergänzt.
Benutzung einer Wasserspiegel – Querschnittsfläche - Abfluss Kennlinie
Ist das Übertragungsverhalten der Transportstrecke durch vorangegangene Wasserspiegellagenberechnung bekannt, kann das Ergebnis in Form einer Wasserspiegel-Querschnitt-Abfluss Kennlinie benutzt werden.
Freispiegel-Rohrleitungen mit nicht-linearem Speicher
Die Berechnung erfolgt mit Hilfe des nicht-linearen Speicherbausteins (Ostrowski (1992)[3]). Der Wellenablauf wird dabei über die Teilfüllungs- bzw. Teilabflusskurve berechnet, wodurch (im Gegensatz zur Berechnung mit dem Kalinin-Miljukov-Verfahren) die nicht-lineare Komponenten des Abflussvorgangs berücksichtigt werden.
Literaturangaben
- ↑ 1.0 1.1 Euler, G. (1983): Ein hydrologisches Näherungsverfahren für die Berechnung des Wellenablaufs in Kreisrohren. Wasser und Boden (Heft 2) (PDF
 )
)
- ↑ Rosemann, H.-J., Vedral, J. (1970): Das Kalinin-Miljukov Verfahren zur Berechnung des Ablaufs von Hochwasserwellen. Schriftenreihe der bayerischen Landesstelle für Gewässerkunde München, Heft 6
- ↑ Ostrowski, M. (1992): Ein universeller Baustein zur Simulation hydrologischer Prozesse, Wasser und Boden, Heft 11 (PDF
 )
)
{{#hierarchy-bottom:}}