Soil moisture calculation

From BlueM
Revision as of 06:45, 9 July 2008 by Froehlich (talk | contribs)
Jump to navigation Jump to search

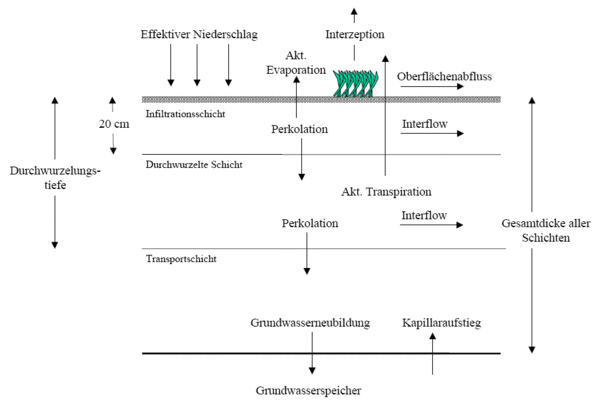
{{#hierarchy-top:}} Alle mit der Bodenfeuchtesimulation berechneten Größen sind im nachfolgenden Bild angegeben.

Abbildung 39: Berechnete Größen mit der Bodenfeuchtsimulation

Bei der Anwendung der Bodenfeuchtesimulation ist die Angabe von Landnutzungen notwendig. Aus den Angaben zur Landnutzung wird die Durchwurzelungstiefe benötigt, um die Dicke der Durchwurzelungsschicht zu ermitteln. Weitere Parameter der Landnutzung, die zur Berechnung der Interzeption und der Transpiration dienen, sind:

  • Wurzeltiefe
  • Bedeckungsgrad
  • Jahresgang des Bedeckungsgrades
  • Blattflächenindex
  • Jahresgang des Blattflächenindexes

Interzeption

In diesem Modell wird der Zufluß zum Interzeptionsspeicher (QzuIz) als lineare Funktion des freien Interzeptionsspeichers beschrieben.

[math]\displaystyle{ Qzu_{IZ} = k \cdot ( IZ_{max} - IZ_{akt}) }[/math]

mit: k : Proportionalitätsfaktor [-] (code-intern = 1)

Die maximale Interzeptionskapazität für landwirtschaftliche Nutzpflanzen geben Hoyningen-Huene [1983]

[math]\displaystyle{ MAXINTC = 0.935 + 0.498 \cdot LAI - 0.00575 \cdot LAI^2 }[/math]

Die Verdunstungsrate EV wird immer mit potentieller Rate angenommen. Da der Zufluß gleich dem Niederschlag über der Vegetation minus dem durchfallendem Niederschlag ist, ergibt sich eine einfache lineare Differentialgleichung:

[math]\displaystyle{ \frac{dIZ_{akt}}{dt} = k \cdot ( IZ_{max} - IZ_{akt}) - EV }[/math]

Durchfallender Niederschlag ergibt sich danach aus der Differenz zwischen dem Niederschlag auf die Vegetation und der Interzeption.

Obwohl der Ansatz aus Untersuchungen von landwirtschaftlichen Nutzpflanzen abgeleitet wurde, wird seine Gültigkeit vereinfacht auch für bewaldete Gebiete angenommen.

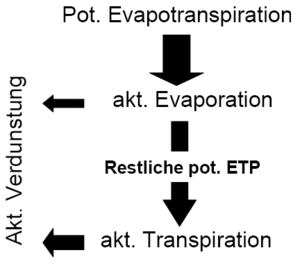
Im Weiteren wird die Interzeptionsverdunstung berechnet. Die ermittelte Interzeptionsverdunstung wird von der potentiellen Verdunstung abgezogen, so dass für die weiteren Prozesse Transpiration und Evaporation nur diese reduzierte potentielle Verdunstung zur Verfügung steht.

Bodenfeuchtesimulation

Die Angabe von Haude-Faktoren[1][2] zur besseren Berücksichtigung der Verdunstung je Landnutzung ist über Eingabe von Jahresgängen beliebig möglich und können den gewünschten Landnutzungen zugeordnet werden.

Diese Haudefaktoren skalieren über ihr Verhältnis zum entsprechenden Haudefaktor für Gras die für den Zeitschritt gültige potentielle Grasreferenzverdunstung.

Bodentyp / Bodenart:

Die Bodenfeuchtesimulation basiert auf einer nichtlinearen Berechnung der einzelnen Bodenhorizonte. Der Boden wird dabei in verschiedene Horizonte (Schichten) eingeteilt. Jede Schicht wird berechnet und mit den (falls vorhanden) darunter bzw. darüber liegenden Schichten abgeglichen. Als Parameter zur Bodenfeuchteberechnung dienen folgende bodenphysikalischen Größen:

  • Welkepunkt (WP)
  • Feldkapazität (FK)
  • Gesamtporenvolumen (GPV)
  • Gesättigte Leitfähigkeit (kf-Wert)
  • Maximale Infiltrationskapazität (Max.Inf.)
  • Maximale Rate des Kapillaraufstiegs (Max.Kap.)
  • Zuordnung zu einer Bodenart: Sand, Schluff, Ton

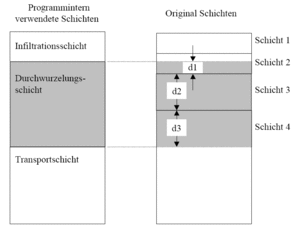
Die mögliche Anzahl der Bodenschichten läuft von minimal einer bis maximal sechs. Die Erfahrung zeigte, dass die besten Ergebnisse mit einer Aufteilung in drei Schichten erzielt werden konnten. Aus diesem Grund werden die eingegebenen Schichten programmintern immer in drei Horizonte unterteilt.

  • Infiltrationsschicht (Standarddicke [cm] = 20)
  • Durchwurzelte Schicht (Mindestdicke [cm] = 5)
  • Transportschicht (Mindestdicke [cm] = 5)

Die Berechnung der neuen Bodenkennwerte für die programmintern verwendeten Schichten erfolgt durch eine Gewichtung entsprechend den vorgegebenen original Dicken der Schichten. Im Fall der gesättigten Leitfähigkeit läuft die Berechnung nach dem Prinzip der Erhaltung der Kontinuität der Strömung ab. Bei senkrechter Strömung soll aufgrund der Kontinuität der Strömung die Geschwindigkeit v bei gegebener Durchflussmenge in einer programminternen Schicht denselben Wert besitzen. Damit ist das hydraulische Gefälle nicht mehr konstant.

Abbildung 38: Beispiel der Zusammenfassung von Bodenschichten anhand der Durchwurzelungsschicht
[math]\displaystyle{ k_{f,v} = \frac{\sum d}{\left ( \frac{d_1}{k_1} + \cdots + \frac{d_i}{k_i} + \cdots + \frac{d_n}{k_n} \right )} }[/math]
mit
di = anteilige Schichtdicke der jeweiligen original Schicht [mm]
ki = gesättigte Leitfähigkeit der jeweiligen original Schicht [mm/h]
kf,v = gesättigte Leitfähigkeit der programmintern verwendeten Schicht [mm/h]

Die Zusammenfassung der Schichten ist in der Abbildung 38 dokumentiert.

Auf der Basis der bereichsweisen linearen Abbildung der die Bodenfeuchte beeinflussenden Prozessfunktionen Infiltration, aktuelle Verdunstung (Evaporation + Transpiration), Perkolation, Interflow und Kapillaraufstieg wird für eine Bodenschicht die Wasserbilanzgleichung gelöst. Die Eingangsgröße für die Evaporation und Transpiration ermittelt sich aus der potentiellen Verdunstung:

Die zu lösende Gleichung ist:

Theorie Abb39b.gif
[math]\displaystyle{ \frac{d\theta(t)}{d\mbox{t}} = \mbox{Inf}(t) - \mbox{Perk}(t) - \mbox{Eva}_{akt}(t) - \mbox{Trans}_{akt}(t) - \mbox{Int}(t) + \mbox{Kap}(t) }[/math]
mit:
θ(t) = aktuelle Bodenfeuchte
Inf(t) = Infiltration in den Boden
Perk(t) = Perkolation (Durchsickerung)
Evaakt(t) = aktuelle Evaporation
Transakt(t) = aktuelle Transpiration
Int(t) = Interflow
Kap(t) = Kapillaraufstieg

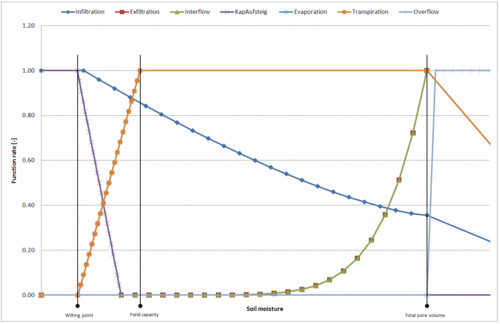
Infiltration, Perkolation, Evaporation, Transpiration, Interflow und Kapillaraufstieg sind von der aktuellen Bodenfeuchte abhängig. In der Simulation wird diese Abhängigkeit durch folgende Funktionsverläufe beschrieben.

Infiltration

[math]\displaystyle{ \mbox{Inf}(\theta(t)) = \mbox{a}_v \cdot \left ( \mbox{GPV} - \theta(t) \right )^{1,4} + k_f }[/math]
(Ansatz nach HOLTAN[3])

Perkolation

Der aktuell verwendete Ansatz:

[math]\displaystyle{ \mbox{Perk}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \\ k_f \cdot \left ( \frac{\theta(t) - \left ( \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \right )}{\mbox{GPV} - \left ( \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \right )} \right )^{n_{PK}}, & \theta(t) \gt \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \end{cases} }[/math]
(mod. Ansatz nach OSTROWSKI, 1992[4], BEAR, 1988[5])

sollte in den Ansatz nach VAN GENUCHTEN[6] geändert werden (siehe Bug 51).

[math]\displaystyle{ \mbox{Perk}(\theta(t)) = k_f \cdot \theta_e^a \cdot \left [ 1 - \left ( 1 - \theta_e^{\frac{n_{PK}}{n_{PK}-1}} \right )^{\frac{n_{PK}-1}{n_{PK}}} \right ]^2 \quad \quad \quad \quad \mbox{mit} \quad a = 0,5 }[/math]
[math]\displaystyle{ \theta_e = \frac{\theta(t)-\mbox{WP}}{\mbox{GPV}-\mbox{WP}} }[/math]
(Ansatz nach WÖSTEN und VAN GENUCHTEN, 1988[7], BENECKE, 1992[8].

Interflow

Der Interflow ist relativ unabhängig von den Bodenparametern und hängt neben der Bodenfeuchte lediglich vom Gefälle der jeweiligen Elementarfläche ab (siehe Bug 28):

[math]\displaystyle{ \mbox{Int}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{1,Int} \cdot \mbox{nFK} \\ \theta(t)^{\mbox{n}_{Int}} \cdot \frac{I}{\sqrt{1+I^2}}, & \mbox{f}_{1,Int} \cdot \mbox{nFK} \lt \theta(t) \le \mbox{f}_{2,Int} \cdot \mbox{nFK} \\ \mbox{f}_{2,Int} \cdot \mbox{nFK}, & \theta(t) \gt \mbox{f}_{2,Int} \cdot \mbox{nFK} \end{cases} }[/math]

Evaporation

Für die Bodenverdunstung wird die an die Landnutzung angepasste, potentielle Verdunstung auf eine potentielle Verdunstung für Brachland umgerechnet.

[math]\displaystyle{ \mbox{Eva}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{WP} \\ \mbox{f}_{Eva} \cdot \left ( \frac{\theta(t)-\mbox{WP}}{\mbox{GPV}-\mbox{WP}} \right ), & \theta(t) \gt \mbox{WP} \end{cases} }[/math]

Transpiration

[math]\displaystyle{ \mbox{Trans}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP} \\ \mbox{f}_{TP} \cdot \left ( \frac{\theta(t) - \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP}}{\mbox{GPV} - \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP}} \right )^{n_{TP}}, & \theta(t) \gt \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP} \end{cases} }[/math]
Abbildung 40: Darstellung ausgewählter Bodenprozessfunktionen
mit:
av = Infiltrationsfaktor nach HOLTAN[3] (in BlueM av = 1)
kf = Durchlässigkeitsbeiwert des gesättigten Bodens
nFK = nutzbare Feldkapazität (nFK = FK - WP)
WP = Welkepunkt
FK = Feldkapazität
GPV = gesamtes Porenvolumen
I = Gefälle [-]
fPK = bodenabhängiger Skalierungsfaktor der Perkolationsfunktion
nPK = bodenabhängiger Krümmungsparameter der Perkolationsfunktion (3 / 7 / 9)
fEva = bodenabhängiger Skalierungsfaktor der Evaporationsfunktion
fTP = bodenabhängiger Skalierungsfaktor der Transpirationsfunktion
f1,Int = bodenabhängiger Skalierungsfaktor für die Interflowfunktion (0.4 / 0.7 / 0.75)
f2,Int = bodenabhängiger Skalierungsfaktor für die Interflowfunktion (0.7 / 0.9 / 0.9)
nInt = bodenabhängiger Krümmungsparameter der Interflowfunktion (2 / 7 / 7)
nTP = Krümmungsparameter der Transpirationsfunktion

Die Programmparameter werden intern berechnet. Der Anwender muss lediglich die Bodenkennwerte kf, WP, FK und GPV angeben.

Die Simulation erfolgt mit einem neu entwickelten Baustein zur Simulation von Speichern, deren Prozessfunktionen bereichsweise linear abzubilden sind.

Elementarflächen:

Abbildung 42: Aufteilung eines Einzugsgebietselementes in Elementarflächen

Wird mit der Bodenfeuchtesimulation die Abflussbildung berechnet, wird gleichzeitig das Elementarflächenkonzept angewandt. Ein Einzugsgebietselement wird dabei in beliebig viele hydrologisch homogene Flächen unterteilt.

Abbildung 42: Zuordnung von Bodentyp und Landnutzung zu Elementarflächen

Für jede Elementarfläche gilt die gezeigte Zuordnung von Landnutzung und Bodentyp. Die aus einer Elementarfläche resultierende Wassermenge wird am Elementausgang angesetzt, d.h. alle Elementarflächen geben unabhängig ihrer Lage im Einzugsgebiet Wasser mit der gleichen zeitlichen Verzögerung ab.

Die Berechnung der Bodenfeuchte ist sehr rechen- und damit auch zeitintensiv. Dies gilt insbesondere dann, wenn viele Elementarflächen je Teilgebiet eingerichtet sind. In TALSIM 2.2 besteht jetzt die Möglichkeit Elementarflächen programmintern aggregieren zu lassen, d.h. nach Vorgabe eines Grenzwertes werden alle Elementarflächen, deren Flächenanteil am Teilgebiet kleiner als der Grenzwert ist zu einer Elementarfläche flächengewichtet zusammengefasst. Dies ist besonders dann sinnvoll, wenn viele Elementarflächen mit Anteilen unter 5% vorhanden sind.

{{#hierarchy-bottom:}}

  1. ↑ Haude, W. (1954): Zur praktischen Bestimmung der aktuellen und potentiellen Evapotranspiration. – Mitt. d. DWD, Bd. 8; Bad Kissingen
  2. ↑ Haude, W. (1955): Zur Bestimmung der Verdunstung auf möglichst einfache Weise. - Mitt. Dt. Wetterd. 2 (11), Bad Kissingen (Dt. Wetterd.)
  3. ↑ 3.0 3.1 Holtan, H.N. (1961): A Concept for Infiltration Estimates in Watershed Engineering, U.S. Department of Agriculture Publication, ARS 41-51.
  4. ↑ Ostrowski, M. (1992): Ein universeller Baustein zur Simulation hydrologischer Prozesse, Wasser und Boden, Heft 11 (PDF information.png)
  5. ↑ Bear, J. (1988): Dynamics of fluids in porous media, American Elsevier Environmental Science Series (books.google.com)
  6. ↑ van Genuchten, M. Th. (1980): A closed-fom equation for predicting the hydraulic conductivity of unsaturated soils - Soil Science Society of America Journal, 44, pp 892-898 (hydro.nevada.edu)
  7. ↑ Wösten, J.H.M., van Genuchten, M. (1988): Using texture and other soil properties to predict the unsaturated soil hydraulic functions, Soil Science Society of America Journal (ars.usda.gov)
  8. ↑ Benecke, P. (1992): Gedanken zur Waldbodenrestaurierung mit Bodenbearbeitung, Allg. Forst Zeitschr., 47:542-545 ???
Retrieved from "https://wiki.bluemodel.org/index.php?title=Soil_moisture_calculation&oldid=5279"