Test problems: Difference between revisions
Jump to navigation
Jump to search
m (needs translation) |
(Translate to english) |
||
| Line 1: | Line 1: | ||
{{BlueM.Opt nav}} | {{BlueM.Opt nav}} | ||
<div style="float:left; margin:0 10px 10px 0;">__TOC__</div> | <div style="float:left; margin:0 10px 10px 0;">__TOC__</div> | ||
List of test problems available in [[BlueM.Opt]]. Some of them are taken from {{:Literature:Moré et al. 1981}}.<br clear="all"/> | |||
==Test problems== | ==Test problems== | ||
=== | ===Sine function=== | ||
Fit parameters to the sine function | |||
===Beale | ===Beale problem=== | ||
[[File:Beale Sensiplot.png|thumb|Beale function (created with [[SensiPlot]])]] | [[File:Beale Sensiplot.png|thumb|Beale function (created with [[SensiPlot]])]] | ||
[[File:Beale_ani.gif|thumb|left|Beale | [[File:Beale_ani.gif|thumb|left|Beale problem being solved with [[PES]]]] | ||
Finding the minimum of the Beale function{{:Literature:Beale 1958|}}. | |||
* Parameters: 2 | * Parameters: 2 | ||
* Objective functions: 1 | * Objective functions: 1 | ||
| Line 17: | Line 16: | ||
<math>f(x,y)=(1.5-x(1-y))^2+(2.25-x(1-y^2))^2+(2.625-x(1-y^3))^2</math> | <math>f(x,y)=(1.5-x(1-y))^2+(2.25-x(1-y^2))^2+(2.625-x(1-y^3))^2</math> | ||
Global | Global minimum: <code>f(3, 0.5) = 0</code><br clear="all" /> | ||
===Schwefel 2.4 | ===Schwefel 2.4 problem=== | ||
Find the minimum (xi=1, F(x)=0) | |||
===Deb 1=== | ===Deb 1=== | ||
Multicriteria test problem (convex) | |||
===Zitzler/Deb T1=== | ===Zitzler/Deb T1=== | ||
Multicriteria test problem (convex) | |||
===Zitzler/Deb T2=== | ===Zitzler/Deb T2=== | ||
Multicriteria test problem (concave) | |||
===Zitzler/Deb T3=== | ===Zitzler/Deb T3=== | ||
[[File:TP ZitzlerDebT3.png|thumb|Zitzler/Deb T3]] | [[File:TP ZitzlerDebT3.png|thumb|Zitzler/Deb T3]] | ||
Multicriteria test problem (convex, non-continuous) | |||
[[File:Zitzler deb t3 ani.gif|thumb|left|Zitzler/Deb T3]]<br clear="all" /> | [[File:Zitzler deb t3 ani.gif|thumb|left|Zitzler/Deb T3]]<br clear="all" /> | ||
===Zitzler/Deb T4=== | ===Zitzler/Deb T4=== | ||
Multicriteria test problem (convex) | |||
===CONSTR=== | ===CONSTR=== | ||
[[File:CONSTR_ani.gif|thumb|CONSTR]] | [[File:CONSTR_ani.gif|thumb|CONSTR]] | ||
Multicriteria test problem (convex) with two contraints<br clear="all" /> | |||
===Box=== | ===Box=== | ||
[[File:EVO Box screenshot.png|thumb|Box]] | [[File:EVO Box screenshot.png|thumb|Box]] | ||
Multicriteria test problem (circle) with two contraints<br clear="all"/> | |||
=== | ===Dependent parameters=== | ||
Parameter dependency: Y > X | |||
===Flood Mitigation=== | ===Flood Mitigation=== | ||
Revision as of 01:54, 19 May 2023
BlueM.Opt | Download | Usage | Development
List of test problems available in BlueM.Opt. Some of them are taken from Moré et al. (1981)[1].
Test problems
Sine function
Fit parameters to the sine function
Beale problem
Beale function (created with SensiPlot)
Beale problem being solved with PES
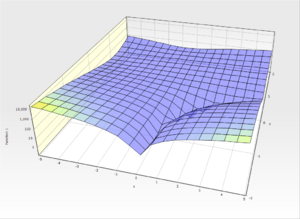
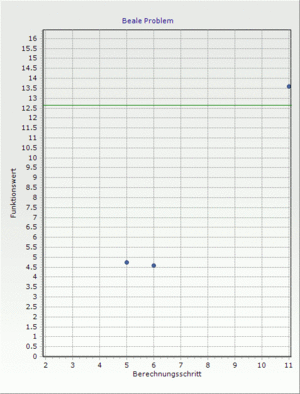
Finding the minimum of the Beale function[2].
- Parameters: 2
- Objective functions: 1
[math]\displaystyle{ f(x,y)=(1.5-x(1-y))^2+(2.25-x(1-y^2))^2+(2.625-x(1-y^3))^2 }[/math]
Global minimum: f(3, 0.5) = 0
Schwefel 2.4 problem
Find the minimum (xi=1, F(x)=0)
Deb 1
Multicriteria test problem (convex)
Zitzler/Deb T1
Multicriteria test problem (convex)
Zitzler/Deb T2
Multicriteria test problem (concave)
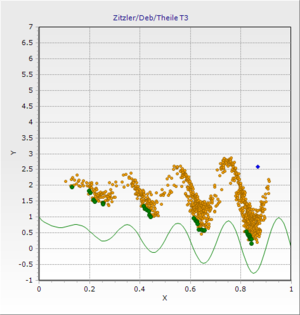
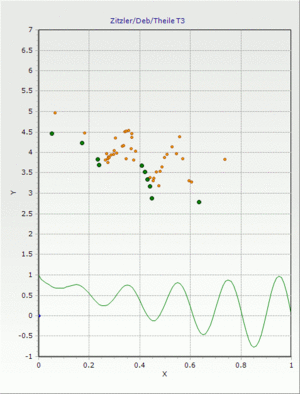
Zitzler/Deb T3
Multicriteria test problem (convex, non-continuous)
Zitzler/Deb T4
Multicriteria test problem (convex)
CONSTR
Multicriteria test problem (convex) with two contraints
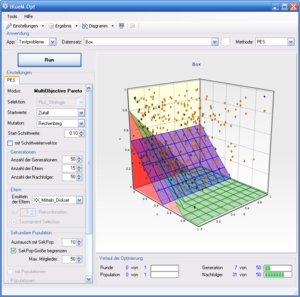
Box
Multicriteria test problem (circle) with two contraints
Dependent parameters
Parameter dependency: Y > X
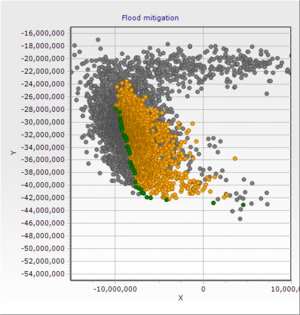
Flood Mitigation
Multicriteria Problem Flood Mitigation and Hydropower Generation[3]
References
- ↑ Moré, J.J., Garbow, B.S. and Hillstrom, K.E. (1981): Testing Unconstrained Optimization Software, ACM Transactions on Mathematical Software (TOMS) 7:1, p. 17-41, doi:10.1145/355934.355936
- ↑ Beale, E. M. L. (1958): On an iterative method of finding a local minimum of a function of more than one variable. Technical Report 25, Statistical Techniques Research Group, Princeton University.
- ↑ Sharma, Ajay (2008): Inflow prediction and optimal operation of reservoir system during flood by the combined application of ANN and different Optimization techniques. Master Thesis, Institute of Hydraulic and Water Resources Engineering, Technische Universität Darmstadt.