Soil moisture calculation

{{#hierarchy-top:}}
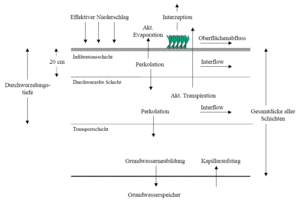
All process-values which are calculated through soil moisture simulation are depicted in the following picture.

Abbildung 39: calculated process-values through soil moisture simulation

Hydrological Response Units (HRUs)

Abbildung 42: Sectioning of a catchment into HRUs

If Runoff is determined through soil moisture simulation, the HRU concept is applied. This results in a catchment being sub-sectioned into a various amount of hydrological homogenous areas.

Abbildung 42: Assignment of soil type and land use to a HRU

The depicted assignment of land use and soil type is valid for each HRU. The resulting amount of water out of a HRU is applied at the outlet of the elemt. Therefore all HRUs discharge their Water with the same time delay, independant of their position within the catchment.

Soil moisture calculation is computationally intensive and therefore very time-consuming. This is especially true if there are many HRUs in each sub-catchment. br clear="all"/>

Land use

Providing information on land use is necessary to run the soil moisture calculation. E.g. the thickness of the rooted zone is determined by providing the root depth in the information regarding land use. Furthermore the parameters of land use are needed to calculate interception and transpiration. The parameters are:

• root depth
• soil coverage
• annual pattern of soil coverage
• leaf area index
• annual pattern of the leaf area index

Providing Haude-Coefficients is possible by providing an annual pattern and assiging them to the desired land use. This allows for a better consideration of evaporation for each land use.

These Haude-Coefficients scale the valid potential grass reference-evaporation for the time step by their ratio to the corresponding Haude-Coefficient for gras.

Soil type

The soil moisture simulation is based on the non-linear calculation of the individual soil layers. The soil is divided into different soil layers. Each layer is calculated and (if existing) adjusted with the layers above or below. The parameters for the soil moisture calculation are the following physical soil properties:

• wilting point (WP)
• field capacity (FK)
• total pore volume (GPV)
• saturated hydraulic-conductivity (kf-Wert)
• maximum infiltration capacity (MaxInf)
• maximum rate of capillary rise (MaxKap)
• Assignment to a soil type: sand, silt, clay

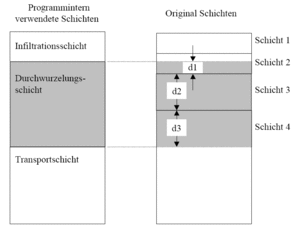
As few as one or as many as six soil layers are possible. A division into three layers has proven to yield the best results. That is why the entered layers are allways distributed into three layers in BlueM internally.

• infiltration layer (standard thickness = 20 [cm])
• root layer (minimum thickness = 5 [cm])
• transport layer (minimum thickness = 5 [cm])

Abbildung 38: Example of the aggregation of soil layers for the root layer

The new characteristic soil parameters for the internally used layers are calculated by weighing the original parameters of the original layers according to the original thickness of these layers.Saturated hydraulic conductivity is calculated according to conservation of continuity of the flow. For vertical Flow the velocity v is to be constant within a layer for a given flow due to the continuity of the flow. Therefore the hydraulic gradient ist no longer constant.

Bei senkrechter Strömung soll aufgrund der Kontinuität der Strömung die Geschwindigkeit v bei gegebener Durchflussmenge in einer programminternen Schicht denselben Wert besitzen. Damit ist das hydraulische Gefälle nicht mehr konstant.

[math]\displaystyle{ k_{f,v} = \frac{\sum d}{\left ( \frac{d_1}{k_1} + \cdots + \frac{d_i}{k_i} + \cdots + \frac{d_n}{k_n} \right )} }[/math]

with

di = depth of each original layer [mm]

ki = saturated hydraulic conductivity of each original layer [mm/h]

kf,v = saturated hydraulic conductivity of the internally used layer [mm/h]

The Aggregation of the layers is depicted in Abbildung 38.

Interception

In BlueM the Inflow to the interception reservoir (QzuIC)is described as a linear function of the free interception reservoir.

[math]\displaystyle{ Q_{zu_{IC}} = k_{IC} \cdot ( \mbox{IC}_{max} - \mbox{IC}_{akt}) }[/math]

with:kIC = 10.0 = Parameter to describe the fill rate of the interception reservoir [1/h] (Bug 409)

The maximum interception capacity for agricultural crops is von Hoyningen-Huene (1983):

[math]\displaystyle{ \mbox{IC}_{max} = 0.935 + 0.498 \cdot LAI - 0.00575 \cdot LAI^2 }[/math]

with

LAI = Leaf Area Index [-]

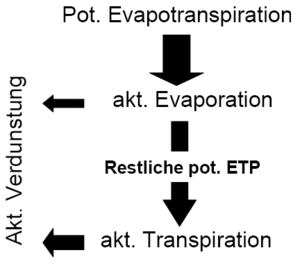
The rate of evaporation is assumed to be equal to the rate of potential evaporation (= ETp).A simple differential equation can be derived due to the fact that inflow is equal to the amount of rain above the vegetation minus the rain which penetrates it :

[math]\displaystyle{ \frac{\mbox{dIC}}{\mbox{d}t} = k_{IC} \cdot ( \mbox{IC}_{max} - \mbox{IC}(t)) - ET_p }[/math]

Therefore the amount of penetrating rain can be determined through the subtraction of interception from rainfall onto the vegetation.

To simplify things it is assumed that this approach is valid for wooded areas, although this approach was derived out of studies for agricultural crops.

Futhermore the interception evaporation is calculated, which is subtracted from the potential evaporation which leads to a reduced potential evaporation remaining for the following processes of transpiration and evaporation.

Soil moisture calculation

The water balance equation for the soil layer is solved by using a stepwise linear approach for the processes effecting soil moisture, whch are Infiltration, Evaporation, Transpiratin, Percolation, Interflow and Capillary-Rise. The input value for evaporation and transpiration is determined through the reduced potential evaporation due to interception evaporation.

The equation to be solved is as follows:

[math]\displaystyle{ \frac{d\theta(t)}{d\mbox{t}} = \mbox{Inf}(t) - \mbox{Perk}(t) - \mbox{Eva}_{akt}(t) - \mbox{Trans}_{akt}(t) - \mbox{Int}(t) + \mbox{Kap}(t) }[/math]

with:

θ(t) = aktuelle Bodenfeuchte

Inf(t) = Infiltration in den Boden

Perk(t) = Perkolation (Durchsickerung)

Evaakt(t) = aktuelle Evaporation

Transakt(t) = aktuelle Transpiration

Int(t) = Interflow

Kap(t) = Kapillaraufstieg

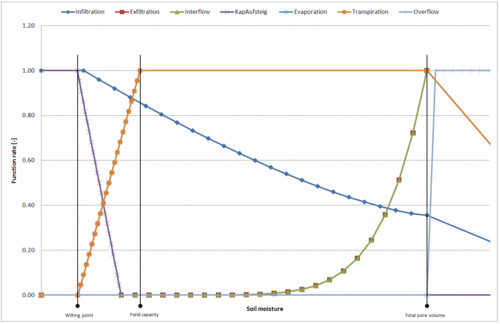
Infiltration, Perkolation, Evaporation, Transpiration, Interflow und Kapillaraufstieg sind von der aktuellen Bodenfeuchte abhängig. In der Simulation wird diese Abhängigkeit durch folgende Funktionsverläufe beschrieben.

Abbildung 40: Darstellung ausgewählter Bodenprozessfunktionen

mit:

kf = Durchlässigkeitsbeiwert des gesättigten Bodens

nFK = nutzbare Feldkapazität (nFK = FK - WP)

WP = Welkepunkt

FK = Feldkapazität

GPV = gesamtes Porenvolumen

I = Gefälle [-]

fPK = bodenabhängiger Skalierungsfaktor der Perkolationsfunktion

fEva = bodenabhängiger Skalierungsfaktor der Evaporationsfunktion

fTP = bodenabhängiger Skalierungsfaktor der Transpirationsfunktion

f1,Int = bodenabhängiger Skalierungsfaktor für die Interflowfunktion

f2,Int = bodenabhängiger Skalierungsfaktor für die Interflowfunktion

nInt = bodenabhängiger Krümmungsparameter der Interflowfunktion

nTP = Krümmungsparameter der Transpirationsfunktion

Die Programmparameter werden intern berechnet. Der Anwender muss lediglich die Bodenkennwerte kf, WP, FK und GPV angeben.

Die Simulation erfolgt mit einem neu entwickelten Baustein zur Simulation von Speichern, deren Prozessfunktionen bereichsweise linear abzubilden sind.

Infiltration

Infiltrationsfunktion in BlueM im Vergleich zur Funktion nach Holtan am Beispiel eines Sandbodens

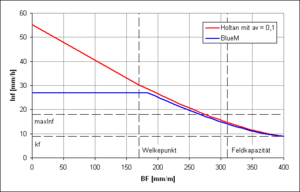
Der ursprüngliche Ansatz nach Holtan (1961):

[math]\displaystyle{ \mbox{Inf}(\theta(t)) = \mbox{a}_v \cdot \left ( \mbox{GPV} - \theta(t) \right )^{1,4} + k_f }[/math]

mit

av = Vegetationsparameter (zwischen 0,1 und 1,0)

wird in BlueM in modifizierter Form angewandt:

[math]\displaystyle{ \mbox{Inf}(\theta(t)) = \begin{cases} \mbox{MaxInf} + k_f, & 0 \lt \theta(t) \lt 0,1 \cdot \mbox{nFK} \\ \mbox{MaxInf} \cdot \left( \frac{\mbox{GPV} - \theta(t)}{\mbox{GPV} - 0,1 \cdot \mbox{nFK}} \right) ^{1,4} + k_f, & \theta(t) \ge 0,1 \cdot \mbox{nFK} \end{cases} }[/math]

wobei zu beachten ist, dass diese Funktion lediglich die potentielle Infiltration beschreibt - die tatsächliche Infiltration wird durch den zur Verfügung stehenden Bestandsniederschlag beschränkt. Die Modifizierung ergibt sich aus der Überlegung, dass bei einem sehr trockenen Boden auf den es regnet, die im Boden vorhande Luft nicht entweichen kann und somit die maximale Infiltration limitiert, sodass dieses nicht weiter exponentiell ansteigt, wie nach dem ursprünglichen Ansatz nach Holtan ("Blumentopfeffekt").

Perkolation

[math]\displaystyle{ \mbox{Perk}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \\ k_f \cdot \left ( \frac{\theta(t) - \left ( \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \right )}{\mbox{GPV} - \left ( \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \right )} \right )^{n_{PK}}, & \theta(t) \gt \mbox{f}_{PK} \cdot \mbox{nFK} + \mbox{WP} \end{cases} }[/math]

mod. Ansatz nach Ostrowski (1992), Bear (1988)

→ zu modifizieren in Ansatz nach van Genuchten

Interflow

Der Interflow ist relativ unabhängig von den Bodenparametern und hängt neben der Bodenfeuchte lediglich vom Gefälle der jeweiligen Elementarfläche ab (siehe Bug 28):

[math]\displaystyle{ \mbox{Int}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{1,Int} \cdot \mbox{nFK} \\ \theta(t)^{\mbox{n}_{Int}} \cdot \frac{I}{\sqrt{1+I^2}}, & \mbox{f}_{1,Int} \cdot \mbox{nFK} \lt \theta(t) \le \mbox{f}_{2,Int} \cdot \mbox{nFK} \\ \mbox{f}_{2,Int} \cdot \mbox{nFK}, & \theta(t) \gt \mbox{f}_{2,Int} \cdot \mbox{nFK} \end{cases} }[/math]

Evaporation

Für die Bodenverdunstung wird die an die Landnutzung angepasste, potentielle Verdunstung auf eine potentielle Verdunstung für Brachland umgerechnet.

[math]\displaystyle{ \mbox{Eva}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{WP} \\ \mbox{f}_{Eva} \cdot \left ( \frac{\theta(t)-\mbox{WP}}{\mbox{GPV}-\mbox{WP}} \right ), & \theta(t) \gt \mbox{WP} \end{cases} }[/math]

Transpiration

[math]\displaystyle{ \mbox{Trans}(\theta(t)) = \begin{cases} 0, & \theta(t) \le \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP} \\ \mbox{f}_{TP} \cdot \left ( \frac{\theta(t) - \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP}}{\mbox{GPV} - \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP}} \right )^{n_{TP}}, & \theta(t) \gt \mbox{f}_{TP} \cdot \mbox{nFK} + \mbox{WP} \end{cases} }[/math]

Literaturangaben

{{#hierarchy-bottom:}}