Test problems: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{BlueM.Opt nav}} | {{BlueM.Opt nav}} | ||
<div style="float: | <div style="float:left; margin:0 10px 10px 0;">__TOC__</div> | ||
Liste der Testprobleme, die in [[BlueM.Opt]] eingebaut sind. Die meisten stammen aus {{:Literature:Moré et al. 1981}}. | Liste der Testprobleme, die in [[BlueM.Opt]] eingebaut sind. Die meisten stammen aus {{:Literature:Moré et al. 1981}}.<br clear="all"/> | ||
==Test problems== | ==Test problems== | ||
===Sinus-Funktion=== | ===Sinus-Funktion=== | ||
Parameter an Sinusfunktion anpassen | Parameter an Sinusfunktion anpassen | ||
===Beale-Problem=== | ===Beale-Problem=== | ||
[[File:Beale Sensiplot.png|thumb | [[File:Beale Sensiplot.png|thumb|Beale-Problem evaluated with [[SensiPlot]]]] | ||
[[File:Beale_ani.gif|thumb|left|Beale-Problem being solved with [[PES]]]] | |||
Es wird das Minimum des Beale-Problems{{:Literature:Beale 1958|}} gesucht. | Es wird das Minimum des Beale-Problems{{:Literature:Beale 1958|}} gesucht. | ||
* Parameters: 2 | * Parameters: 2 | ||
| Line 16: | Line 16: | ||
<math>f(x,y)=(1.5-x(1-y))^2+(2.25-x(1-y^2))^2+(2.625-x(1-y^3))^2</math> | <math>f(x,y)=(1.5-x(1-y))^2+(2.25-x(1-y^2))^2+(2.625-x(1-y^3))^2</math> | ||
Global Minimum: <code>f(3, 0.5) = 0</code> | Global Minimum: <code>f(3, 0.5) = 0</code><br clear="all" /> | ||
===Schwefel 2.4-Problem=== | ===Schwefel 2.4-Problem=== | ||
Revision as of 03:39, 11 September 2009
 BlueM.Opt | Download | Usage | Development
BlueM.Opt | Download | Usage | Development
Liste der Testprobleme, die in BlueM.Opt eingebaut sind. Die meisten stammen aus Moré et al. (1981)[1].
Test problems
Sinus-Funktion
Parameter an Sinusfunktion anpassen
Beale-Problem
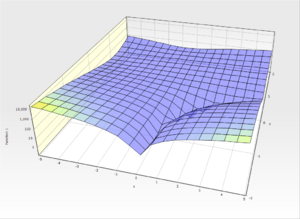
Es wird das Minimum des Beale-Problems[2] gesucht.
- Parameters: 2
- Objective functions: 1
[math]\displaystyle{ f(x,y)=(1.5-x(1-y))^2+(2.25-x(1-y^2))^2+(2.625-x(1-y^3))^2 }[/math]
Global Minimum: f(3, 0.5) = 0
Schwefel 2.4-Problem
Minimum der Problemstellung wird gesucht (xi=1, F(x)=0)
Deb 1
Multikriterielles Testproblem (konvex)
Zitzler/Deb T1
Multikriterielles Testproblem (konvex)
Zitzler/Deb T2
Multikriterielles Testproblem (konkav)
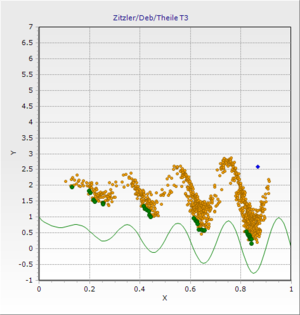
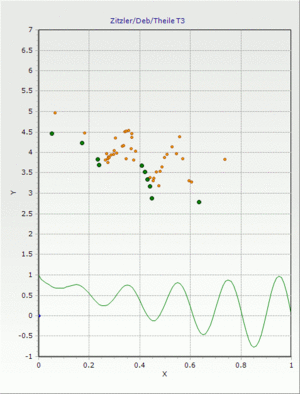
Zitzler/Deb T3
Multikriterielles Testproblem (konvex, nicht stetig)
Zitzler/Deb T4
Multikriterielles Testproblem (konvex)
CONSTR
Multikriterielles Testproblem (konvex) mit zwei Randbedingungen
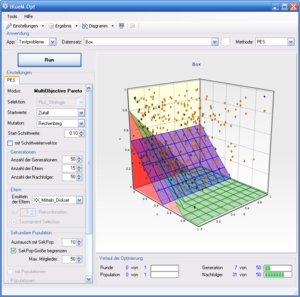
Box
Multikriterielles Testproblem (Kreis) mit zwei Randbedingungen
Abhängige Parameter
Bedingung im Parameterraum: Y > X
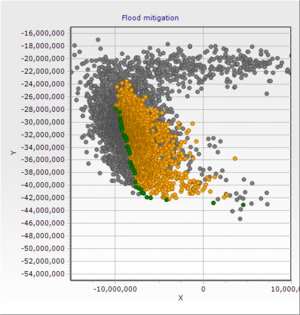
Flood Mitigation
Multicriteria Problem Flood Mitigation and Hydropower Generation[3]
References
- ↑ Moré, J.J., Garbow, B.S. and Hillstrom, K.E. (1981): Testing Unconstrained Optimization Software, ACM Transactions on Mathematical Software (TOMS) 7:1, p. 17-41, doi:10.1145/355934.355936
- ↑ Beale, E. M. L. (1958): On an iterative method of finding a local minimum of a function of more than one variable. Technical Report 25, Statistical Techniques Research Group, Princeton University.
- ↑ Sharma, Ajay (2008): Inflow prediction and optimal operation of reservoir system during flood by the combined application of ANN and different Optimization techniques. Master's Thesis.