Test problems: Difference between revisions
(→Zitzler/Deb T3: remove second image) |
(Added Ackley function (BlueM.Opt v2.4.0)) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
==Test problems== | ==Test problems== | ||
===Ackley function=== | |||
[[File:BlueM.Opt Ackley function.png|thumb|right|Ackley function]] | |||
The Ackley function is a non-convex function used as a performance test problem for optimization algorithms. It was proposed by David Ackley in his 1987 PhD dissertation{{:Literature:Ackley 1987|}}. | |||
On a 2-dimensional domain it is defined by: | |||
: <math> | |||
\begin{align} | |||
f(x,y) = -20&{}\exp\left[-0.2\sqrt{0.5(x^2+y^2)}\,\right] \\ | |||
& {} -\exp\left[0.5\left(\cos 2\pi x + \cos 2\pi y \right)\right] + e + 20 | |||
\end{align} | |||
</math>{{:Literature:Bäck 1996|}} | |||
Its global optimum point is | |||
:<math>f(0,0) = 0.</math><br clear="all" /> | |||
===Beale problem=== | ===Beale problem=== | ||
[[File:Beale Sensiplot.png|thumb|Beale function (created with [[SensiPlot]])]] | [[File:Beale Sensiplot.png|thumb|right|Beale function (created with [[SensiPlot]])]] | ||
[[File:Beale_ani.gif|thumb| | [[File:Beale_ani.gif|thumb|right|Beale problem being solved with [[PES]] (animation)]] | ||
Finding the minimum of the Beale function{{:Literature:Beale 1958|}}. | Finding the minimum of the Beale function{{:Literature:Beale 1958|}}. | ||
* Parameters: 2 | * Parameters: 2 | ||
| Line 21: | Line 38: | ||
===CONSTR=== | ===CONSTR=== | ||
[[File:CONSTR_ani.gif|thumb|CONSTR]] | [[File:CONSTR_ani.gif|thumb|CONSTR]] | ||
Multicriteria test problem (convex) with two | Multicriteria test problem (convex) with two constraints<br clear="all" /> | ||
===Deb 1=== | ===Deb 1=== | ||
Latest revision as of 01:18, 19 May 2023
 BlueM.Opt | Download | Usage | Development
BlueM.Opt | Download | Usage | Development
List of test problems available in BlueM.Opt. Some of them are taken from Moré et al. (1981)[1].
Test problems
Ackley function
The Ackley function is a non-convex function used as a performance test problem for optimization algorithms. It was proposed by David Ackley in his 1987 PhD dissertation[2].
On a 2-dimensional domain it is defined by:
- [math]\displaystyle{ \begin{align} f(x,y) = -20&{}\exp\left[-0.2\sqrt{0.5(x^2+y^2)}\,\right] \\ & {} -\exp\left[0.5\left(\cos 2\pi x + \cos 2\pi y \right)\right] + e + 20 \end{align} }[/math][3]
Its global optimum point is
- [math]\displaystyle{ f(0,0) = 0. }[/math]
Beale problem
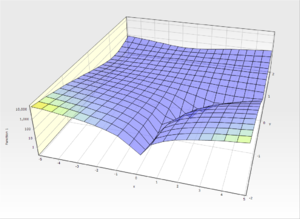
Finding the minimum of the Beale function[4].
- Parameters: 2
- Objective functions: 1
[math]\displaystyle{ f(x,y)=(1.5-x(1-y))^2+(2.25-x(1-y^2))^2+(2.625-x(1-y^3))^2 }[/math]
Global minimum: f(3, 0.5) = 0
Box
Multicriteria test problem (circle) with two contraints
CONSTR
Multicriteria test problem (convex) with two constraints
Deb 1
Multicriteria test problem (convex)
Dependent parameters
Parameter dependency: Y > X
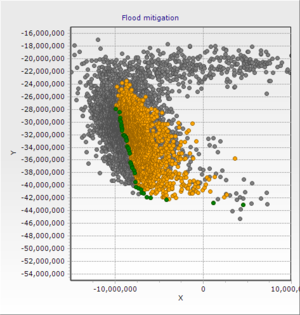
Flood Mitigation
Multicriteria Problem Flood Mitigation and Hydropower Generation[5]
Schwefel 2.4 problem
Find the minimum (xi=1, F(x)=0)
Sine function
Fit parameters to the sine function
Zitzler/Deb T1
Multicriteria test problem (convex)
Zitzler/Deb T2
Multicriteria test problem (concave)
Zitzler/Deb T3
Multicriteria test problem (convex, non-continuous)
Zitzler/Deb T4
Multicriteria test problem (convex)
References
- ↑ Moré, J.J., Garbow, B.S. and Hillstrom, K.E. (1981): Testing Unconstrained Optimization Software, ACM Transactions on Mathematical Software (TOMS) 7:1, p. 17-41, doi:10.1145/355934.355936
- ↑ Ackley, D. H. (1987): "A connectionist machine for genetic hillclimbing", Kluwer Academic Publishers, Boston MA.
- ↑ Bäck, Thomas (1996): "Artificial Landscapes". Evolutionary Algorithms in Theory and Practice. Oxford University Press. p. 142. doi:10.1093/oso/9780195099713.003.0008. ISBN 978-0-19-509971-3.
- ↑ Beale, E. M. L. (1958): On an iterative method of finding a local minimum of a function of more than one variable. Technical Report 25, Statistical Techniques Research Group, Princeton University.
- ↑ Sharma, Ajay (2008): Inflow prediction and optimal operation of reservoir system during flood by the combined application of ANN and different Optimization techniques. Master Thesis, Institute of Hydraulic and Water Resources Engineering, Technische Universität Darmstadt.