SCS-Method: Difference between revisions
(übernommen aus Natürliche Einzugsgebiete) |
(weitere Teile aus Diskussion:Natürliche_Einzugsgebiete übernommen) |
||
| Line 1: | Line 1: | ||
{{HierarchieKopf}} | {{HierarchieKopf}} | ||
'''<big>Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)</big>''' | '''<big>Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)</big>''' | ||
__TOC__ | |||
==Theorie== | |||
Das in BlueM verwendete Verfahren ist eine Weiterentwicklung nach {{:Literatur:Zaiß_1989}} der ursprünglichen ''Curve Number Method'' ({{:Literatur:USDA_1964}}). | |||
[[Bild:Theorie_Abb36.gif|thumb|Abbildung 36: Abhängigkeit des Abflussbeiwertes von der Vorgeschichte]] | [[Bild:Theorie_Abb36.gif|thumb|Abbildung 36: Abhängigkeit des Abflussbeiwertes von der Vorgeschichte]] | ||
Bei Angabe eines vom Bodentyp und der Bodennutzung abhängigen CN-Wertes (siehe {{:Literatur:DVWK_1991}}) lässt sich ein vorgeschichtsabhängiger Anfangsverlust sowie eine vorgeschichtsabhängige Beziehung des Abflussbeiwertes von der bis zum betrachteten Zeitpunkt akkumulierten Niederschlagshöhe formulieren; d.h. der Abflussbeiwert wächst mit zunehmendem Niederschlag im Verlauf des Ereignisses an. | |||
In Abhängigkeit von der auf diese Weise quantifizierten Vorgeschichte kann unter Verwendung der gebietsspezifischen und für mittlere Vorfeuchteverhältnisse gültigen CN-Werte ein aktueller Abflussbeiwert berechnet werden. In [[:Bild:Theorie_Abb36.gif|Abbildung 36]] ist für unterschiedliche CN-Werte dargestellt, wie sich der aktuelle Abflussbeiwert in Abhängigkeit von der Vorgeschichte verändert. | In Abhängigkeit von der auf diese Weise quantifizierten Vorgeschichte kann unter Verwendung der gebietsspezifischen und für mittlere Vorfeuchteverhältnisse gültigen CN-Werte ein aktueller Abflussbeiwert berechnet werden. In [[:Bild:Theorie_Abb36.gif|Abbildung 36]] ist für unterschiedliche CN-Werte dargestellt, wie sich der aktuelle Abflussbeiwert in Abhängigkeit von der Vorgeschichte verändert. | ||
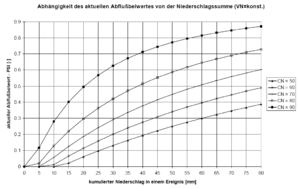
[[Bild:Theorie_Abb37.gif|thumb|Abbildung 37: Abhängigkeit des Abflussbeiwertes von der kumulierten Niederschlagssumme]] | [[Bild:Theorie_Abb37.gif|thumb|Abbildung 37: Abhängigkeit des Abflussbeiwertes von der kumulierten Niederschlagssumme]] | ||
Da sich im Verlaufe eines Regenereignisses durch die Durchfeuchtung des Bodens die Abflussbereitschaft eines Einzugsgebiets verändert, wird ebenfalls eine Anpassung des Abflussbeiwertes während eines Ereignisses als Funktion der kumulierten Niederschlagshöhe vorgenommen. In [[:Bild:Theorie_Abb37.gif|Abbildung 37]] ist dieser Zusammenhang für unterschiedliche CN-Werte dargestellt. | Da sich im Verlaufe eines Regenereignisses durch die Durchfeuchtung des Bodens die Abflussbereitschaft eines Einzugsgebiets verändert, wird ebenfalls eine Anpassung des Abflussbeiwertes während eines Ereignisses als Funktion der kumulierten Niederschlagshöhe vorgenommen. In [[:Bild:Theorie_Abb37.gif|Abbildung 37]] ist dieser Zusammenhang für unterschiedliche CN-Werte dargestellt. | ||
| Line 40: | Line 23: | ||
Eine weitere Möglichkeit zur Beeinflussung der Abflussbildung besteht in der Option, einen Endabflussbeiwert festzulegen. Damit beschränkt man unabhängig vom gewählten Verlustansatz den maximalen Abflussbeiwert. Standardmäßig setzt TALSIM den Endabflussbeiwert auf 1. | Eine weitere Möglichkeit zur Beeinflussung der Abflussbildung besteht in der Option, einen Endabflussbeiwert festzulegen. Damit beschränkt man unabhängig vom gewählten Verlustansatz den maximalen Abflussbeiwert. Standardmäßig setzt TALSIM den Endabflussbeiwert auf 1. | ||
</div> | </div> | ||
==Berechnung== | |||
===Einmalig berechnete Parameter=== | |||
'''Eingangsgröße:''' <code>CN<sub>II</sub></code> | |||
<div class="comment"> | |||
Die Umrechnung von <code>CN<sub>II</sub></code> in <code>CN<sub>I</sub></code> bedeutet, dass davon ausgegangen wird, dass das Gebiet zu Beginn der Simulation trocken ist?! | |||
</div> | |||
'''Umrechnung''' von <code>CN<sub>II</sub></code> in <code>CN<sub>I</sub></code>: | |||
:<math>CN_I = \frac{CN_{II}}{(2.3340 - 0.01334 \cdot CN_{II})}</math> | |||
'''Maximaler Gebietsrückhalt''' (Speichervermögen) <code>S<sub>max</sub></code> [mm]: | |||
:<math>S_{max} = \frac{25400}{CN_I} - 254</math> | |||
'''Gebietsspezifischer Anfangsverlust''' <code>I<sub>a</sub></code> [mm]: | |||
:<math>I_a = a \cdot S_{max}</math> | |||
:mit | |||
:<code>a</code> = Konstante, ursprünglich mit <code>0,2</code> angenommen{{:Literatur:USDA_1964|}}, in BlueM für europäische Verhältnisse angepasst an <code>0,05</code>{{:Literatur:DVWK_1991|}} | |||
'''Krümmungsparameter''' <code>CVW</code>: | |||
<div class="comment"> | |||
Laut {{:Literatur:Sartor_1999|Sartor}}, der die selbe Gleichung verwendet, stammt dieser Ansatz aus der Dokumentation von SMUSI 3.0 | |||
</div> | |||
:<math>CVW = \frac{-100.}{\ln(\frac{0.5}{I_a})}</math> | |||
:''entspricht <code>b<sub>1</sub></code> in Gl. 4.5b in {{:Literatur:Zaiß_1989}}'' | |||
:laut Zaiß: | |||
<blockquote> | |||
Eine Abhängigkeit des "Krümmungsparameters" b<sub>1</sub> von Gebietskenngrößen konnte im Rahmen dieser Arbeit nicht gefunden werden. Sie läßt sich nach den hier aufgeführten Zusammenhängen lediglich über Regressionsanalysen mehrerer N-A-Ereignisse für das jeweils betreffende Einzugsgebiet ermitteln. | |||
</blockquote> | |||
===kontinuierlich berechnete Parameter=== | |||
====Vorgeschichte==== | |||
Die Quantifizierung der Vorgeschichte erfolgt über den 21-Tage-Vorregenindex <code>V<sub>N</sub></code>: | |||
:<math>V_N = \sum_{j=0}^{21} C(j)^j \cdot h_{N,j}</math> | |||
:''Gl. 2.1 in {{:Literatur:Zaiß_1989}}'' | |||
:mit | |||
:<code>h<sub>N,j</sub></code> = Niederschlagshöhe des j-ten Vortags (<code>j = 0</code> ist aktueller Tag) | |||
:<code>C(j)</code> = Faktor, der den Einfluss des j-ten Vortags beschreibt | |||
Der Einfluss der Jahreszeit wird durch einen Jahresgang des Faktors C wiedergegeben. | |||
:<math>C = 0.85 \cdot \sin\left(\frac{2 \pi}{365}\right) (i + 0.75 ) + 0.85</math> | |||
:''Quelle? bei Zaiß finden sich nur so ähnliche Formeln (2.2 & 2.3)'' | |||
:mit | |||
:<code>i</code> = lfd. Tag des Abflussjahres | |||
Damit schwankt der Wert <code>C</code> zwischen <code>0,8 < C < 0,9</code>. Hierdurch wird erreicht, dass bei gleichem Vorregen zu unterschiedlichen Jahreszeiten unterschiedliche Vorregenindizes berechnet und damit eine veränderte Abflussbereitschaft in Rechnung gestellt wird. | |||
====Ereignisspezifischer Anfangsverlust==== | |||
:<math>h_{va} = I_a \cdot e^{-\frac{V_N}{CVW}}</math> | |||
:''Gl. 4.5b in {{:Literatur:Zaiß_1989}}'' | |||
====Abflussbeiwert==== | |||
[[Bild:SCS PSI.png|thumb|Abhängigkeit von <code>ψ</code> zu <code>h<sub>va</sub></code> und <code>h<sub>NE</sub></code> (mit <code>A<sub>v</sub> = 0.05</code>)]] | |||
:<math>\psi = \begin{cases} | |||
0, & h_{va} \ge h_{NE} \\ | |||
1 - \left(\frac{h_{va}}{A_v \cdot h_{NE} + (1 - A_v) \cdot h_{va}}\right)^2, & h_{va} < h_{NE} | |||
\end{cases}</math> | |||
:''Gl. 4.4 in {{:Literatur:Zaiß_1989}}'' | |||
:mit | |||
: <code>A<sub>v</sub></code> = Verlustverhältnis = <code>0,05</code> | |||
: <code>h<sub>NE</sub></code> = ereignisbezogene Summe des Niederschlags [mm] | |||
==Literaturangaben== | |||
<references/> | |||
{{HierarchieFuss}} | {{HierarchieFuss}} | ||
[[Kategorie:BlueM Theorie]] | [[Kategorie:BlueM Theorie]] | ||
Revision as of 04:44, 19 November 2008
{{#hierarchy-top:}} Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)
Theorie
Das in BlueM verwendete Verfahren ist eine Weiterentwicklung nach Zaiß (1989)[1] der ursprünglichen Curve Number Method (USDA (1964)[2]).
Bei Angabe eines vom Bodentyp und der Bodennutzung abhängigen CN-Wertes (siehe DVWK (1991)[3]) lässt sich ein vorgeschichtsabhängiger Anfangsverlust sowie eine vorgeschichtsabhängige Beziehung des Abflussbeiwertes von der bis zum betrachteten Zeitpunkt akkumulierten Niederschlagshöhe formulieren; d.h. der Abflussbeiwert wächst mit zunehmendem Niederschlag im Verlauf des Ereignisses an.
In Abhängigkeit von der auf diese Weise quantifizierten Vorgeschichte kann unter Verwendung der gebietsspezifischen und für mittlere Vorfeuchteverhältnisse gültigen CN-Werte ein aktueller Abflussbeiwert berechnet werden. In Abbildung 36 ist für unterschiedliche CN-Werte dargestellt, wie sich der aktuelle Abflussbeiwert in Abhängigkeit von der Vorgeschichte verändert.
Da sich im Verlaufe eines Regenereignisses durch die Durchfeuchtung des Bodens die Abflussbereitschaft eines Einzugsgebiets verändert, wird ebenfalls eine Anpassung des Abflussbeiwertes während eines Ereignisses als Funktion der kumulierten Niederschlagshöhe vorgenommen. In Abbildung 37 ist dieser Zusammenhang für unterschiedliche CN-Werte dargestellt.
Bei der Abhängigkeit der Abflussbereitschaft zum kumulierten Niederschlag bietet TALSIM 2.2 zwei Möglichkeiten:
- Variabler Verlustansatz (default):
Die Anpassung eines Verlustwertes für die Funktion des Abflussbeiwertes zum kumulierten Niederschlag erfolgt für jeden Zeitschritt neu.
(liefert insgesamt höhere Abflussbeiwerte, so dass auf die Berücksichtigung eines Vorregens verzichtet werden kann) - Konstanter Verlustansatz:
Die Anpassung des Verlustwertes erfolgt nur zu Ereignisbeginn einmalig.
(der Ansatz eines Vorregens ist in diesem Fall zweckmäßig)
Welcher Ansatz bessere Ergebnisse liefert geht nur aus einem Vergleich mit gemessenen Ganglinien hervor. Grundsätzlich ergeben sich mit dem variablen Verlustansatz höhere Abflussspitzen und Füllen bei gleichen Bedingungen.
Eine weitere Möglichkeit zur Beeinflussung der Abflussbildung besteht in der Option, einen Endabflussbeiwert festzulegen. Damit beschränkt man unabhängig vom gewählten Verlustansatz den maximalen Abflussbeiwert. Standardmäßig setzt TALSIM den Endabflussbeiwert auf 1.
Berechnung
Einmalig berechnete Parameter
Eingangsgröße: CNII
Umrechnung von CNII in CNI:
- [math]\displaystyle{ CN_I = \frac{CN_{II}}{(2.3340 - 0.01334 \cdot CN_{II})} }[/math]
Maximaler Gebietsrückhalt (Speichervermögen) Smax [mm]:
- [math]\displaystyle{ S_{max} = \frac{25400}{CN_I} - 254 }[/math]
Gebietsspezifischer Anfangsverlust Ia [mm]:
- [math]\displaystyle{ I_a = a \cdot S_{max} }[/math]
- mit
a= Konstante, ursprünglich mit0,2angenommen[2], in BlueM für europäische Verhältnisse angepasst an0,05[3]
Krümmungsparameter CVW:
Laut Sartor[4], der die selbe Gleichung verwendet, stammt dieser Ansatz aus der Dokumentation von SMUSI 3.0
- [math]\displaystyle{ CVW = \frac{-100.}{\ln(\frac{0.5}{I_a})} }[/math]
- entspricht
b1in Gl. 4.5b in Zaiß (1989)[5] - laut Zaiß:
Eine Abhängigkeit des "Krümmungsparameters" b1 von Gebietskenngrößen konnte im Rahmen dieser Arbeit nicht gefunden werden. Sie läßt sich nach den hier aufgeführten Zusammenhängen lediglich über Regressionsanalysen mehrerer N-A-Ereignisse für das jeweils betreffende Einzugsgebiet ermitteln.
kontinuierlich berechnete Parameter
Vorgeschichte
Die Quantifizierung der Vorgeschichte erfolgt über den 21-Tage-Vorregenindex VN:
- [math]\displaystyle{ V_N = \sum_{j=0}^{21} C(j)^j \cdot h_{N,j} }[/math]
- Gl. 2.1 in Zaiß (1989)[6]
- mit
hN,j= Niederschlagshöhe des j-ten Vortags (j = 0ist aktueller Tag)C(j)= Faktor, der den Einfluss des j-ten Vortags beschreibt
Der Einfluss der Jahreszeit wird durch einen Jahresgang des Faktors C wiedergegeben.
- [math]\displaystyle{ C = 0.85 \cdot \sin\left(\frac{2 \pi}{365}\right) (i + 0.75 ) + 0.85 }[/math]
- Quelle? bei Zaiß finden sich nur so ähnliche Formeln (2.2 & 2.3)
- mit
i= lfd. Tag des Abflussjahres
Damit schwankt der Wert C zwischen 0,8 < C < 0,9. Hierdurch wird erreicht, dass bei gleichem Vorregen zu unterschiedlichen Jahreszeiten unterschiedliche Vorregenindizes berechnet und damit eine veränderte Abflussbereitschaft in Rechnung gestellt wird.
Ereignisspezifischer Anfangsverlust
- [math]\displaystyle{ h_{va} = I_a \cdot e^{-\frac{V_N}{CVW}} }[/math]
- Gl. 4.5b in Zaiß (1989)[7]
Abflussbeiwert
- [math]\displaystyle{ \psi = \begin{cases} 0, & h_{va} \ge h_{NE} \\ 1 - \left(\frac{h_{va}}{A_v \cdot h_{NE} + (1 - A_v) \cdot h_{va}}\right)^2, & h_{va} \lt h_{NE} \end{cases} }[/math]
- Gl. 4.4 in Zaiß (1989)[8]
- mit
Av= Verlustverhältnis =0,05hNE= ereignisbezogene Summe des Niederschlags [mm]
Literaturangaben
- ↑ Zaiß, H. (1989): Simulation ereignisspezifischer Einflüsse des Niederschlag-Abfluß-Prozesses von Hochwasserereignissen kleiner Einzugsgebiete mit N-A-Modellen. Technischer Bericht des Instituts für Ingenieurhydrologie und Hydraulik, TH Darmstadt, Nr. 42
- ↑ 2.0 2.1 U.S. Department of Agriculture, Soil Conservation Service (1964): National Engineering Handbook, Section 4 Hydrology, Washington
(überarbeitete Fassung von 2004: NEH Part 630 Ch. 10) - ↑ 3.0 3.1 DVWK (1991): Beitrag zur Bestimmung des effektiven Niederschlags für Bemessungshochwasser aus Gebietskenngrößen. Ergebnis einer vergleichenden Untersuchung durch den DVWK-Fachausschuß "Niederschlag-Abfluß-Modelle", Materialien, Heft 2
- ↑ Sartor, J. (1999): Einsatz der Langzeit-Seriensimulation für kleine Einzugsgebiete, In: Berichte des Fachgebietes Wasserbau und Wasserwirtschaft der Universität Kaiserslautern, Heft 9 (PDF)
- ↑ Zaiß, H. (1989): Simulation ereignisspezifischer Einflüsse des Niederschlag-Abfluß-Prozesses von Hochwasserereignissen kleiner Einzugsgebiete mit N-A-Modellen. Technischer Bericht des Instituts für Ingenieurhydrologie und Hydraulik, TH Darmstadt, Nr. 42
- ↑ Zaiß, H. (1989): Simulation ereignisspezifischer Einflüsse des Niederschlag-Abfluß-Prozesses von Hochwasserereignissen kleiner Einzugsgebiete mit N-A-Modellen. Technischer Bericht des Instituts für Ingenieurhydrologie und Hydraulik, TH Darmstadt, Nr. 42
- ↑ Zaiß, H. (1989): Simulation ereignisspezifischer Einflüsse des Niederschlag-Abfluß-Prozesses von Hochwasserereignissen kleiner Einzugsgebiete mit N-A-Modellen. Technischer Bericht des Instituts für Ingenieurhydrologie und Hydraulik, TH Darmstadt, Nr. 42
- ↑ Zaiß, H. (1989): Simulation ereignisspezifischer Einflüsse des Niederschlag-Abfluß-Prozesses von Hochwasserereignissen kleiner Einzugsgebiete mit N-A-Modellen. Technischer Bericht des Instituts für Ingenieurhydrologie und Hydraulik, TH Darmstadt, Nr. 42
{{#hierarchy-bottom:}}


Die Umrechnung von
CNIIinCNIbedeutet, dass davon ausgegangen wird, dass das Gebiet zu Beginn der Simulation trocken ist?!