Transport elements

{{#hierarchy-top:}}

Transportstrecken bilden das Translations-und Retentionsverhalten natürlicher Gewässerläufe oder Rohrleitungen ab. Dabei unterscheiden sich die Ansätze zur Berechnung von Rohren oder natürlichen Gerinnen.

Abbildung 45: Berechnungsoptionen für das Transportelement

• Translation (Option 1):

Die Zulaufwelle wird mit einem zeitlichen Versatz, welcher der Fließzeit in der Transportstrecke entspricht, an den Auslauf verschoben. Ist die Fließzeit kleiner als der Berechnungszeitschritt, wird in den Simulationsergebnissen das Translationsverhalten nicht sichtbar.

• Freispiegel-Rohrleitungen (Option 2):

Es erfolgt eine Wellenablaufberechnung für Rohre nach Kalinin-Miljukov. Die Parameter des Kalinin-Miljukov-Verfahrens werden programmintern nach Euler, 1983 für Kreisrohre abgeschätzt, bzw. für nicht kreisförmige Profile unter Angabe des hydraulischen Durchmessers und der Querschnittsfläche bei Vollfüllung bestimmt.

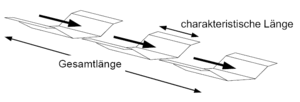
charakteristische Länge:	[math]\displaystyle{ L = 0.4 \cdot \frac{D}{I_S} \quad [\mbox{m}] }[/math]
Retentionskonstante:	[math]\displaystyle{ K = 0.64 \cdot L \cdot \frac{D^2}{Q_v} \quad [\mbox{s}] }[/math]

mit

D [m] = Kreisrohrdurchmesser bzw. hydraulischer Durchmesser

I_S [-] = Sohlgefälle des Rohres

Q_v [m³/s] = scheitelvolle Abflussleistung des Rohres

Die scheitelvolle Abflussleistung des Rohres wird nach dem Fließgesetz von Prandtl-Colebrook berechnet:

[math]\displaystyle{ Q_v = A_v \left [ -2 \cdot \lg \left [ \frac{2.51 \cdot \nu}{D\sqrt{2gDI_S}}+\frac{k_b}{3.71 \cdot b} \right ] \cdot \sqrt{2gDI_S} \right ] }[/math]

mit:

A_v [m²] = Querschnittsfläche des Profils

ν [m²/s] = kinematische Viskosität

k_b [m] = Betriebsrauheit

g [m/s²] = Erdbeschleunigung

Entsprechend der charakteristischen Länge L wird die Gesamtlänge L_g des Sammlers in n gleichlange Berechnungsabschnitte unterteilt mit

[math]\displaystyle{ n = \frac{L_g}{L} }[/math] (wobei n eine ganze Zahl ist)

Für die einzelnen Berechnungsabschnitte gelten die angepassten Parameter

[math]\displaystyle{ L^* = \frac{L_g}{n} }[/math]

[math]\displaystyle{ K^* = K \cdot \frac{L^*}{L} }[/math]

Basierend auf diesen Parametern wird nach n-fachem Durchlaufen der Rekursionsformel

[math]\displaystyle{ Q_{a,i} = Q_{a,i-1} + C_1 \cdot (Q_{z,i-1} - Q_{a,i-1}) + C_2 \cdot (Q_{z,i} - Q_{z,i-1}) }[/math]

mit

Q_z = Zufluss zum Berechnungsabschnitt

Q_a = Abfluss aus Berechnungsabschnitt

i = aktueller Berechnungszeitschritt

i-1 = vorheriger Berechnungszeitschnitt

dt = Berechnungszeitintervall

[math]\displaystyle{ C_1 = 1 - e^{-\frac{dt}{K^*}} }[/math]

[math]\displaystyle{ C_2 = 1 - \frac{\frac{K^*}{dt}}{C_1} }[/math]

der Abfluss am unteren Sammlerende berechnet.

Dieses von Kalinin-Miljukov abgeleitete Näherungsverfahren ist nichts anderes als die bei der Abflusskonzentration verwendete Speicherkaskade; d.h. der Wellenablauf in einer Transportstrecke lässt sich durch eine Speicherkaskade bestehend aus n Speichern mit der Speicherkonstante K^* simulieren.

• offene Gerinne mit Angabe eines Querprofils (Option 3):

Auch hier wird mit Hilfe der Wellenablaufberechnung nach Kalinin-Miljukov das Translations- und Retentionsverhalten abgebildet. Aus der Normalabflussbeziehung nach Manning-Strickler wird die charakteristische Länge als Parameter des Kalinin-Miljukov-Verfahrens abgeleitet (Rosemann, 1970).

Mit der charakteristischen Länge erfolgt für das Gerinne eine Aufteilung in einzelne Segmente. Für jedes Segment wird mit Hilfe der Normalabflussbeziehung über eine nichtlineare Speicherberechnung (siehe Bodenfeuchtesimulation) die Berechnung des Übertragungsverhaltens vollzogen.

• Benutzung einer Wasserspiegel – Querschnittsfläche - Abfluss Kennlinie (Option 4):

Ist das Übertragungsverhalten der Transportstrecke durch vorangegangene Wasserspiegellagenberechnung bekannt, kann das Ergebnis in Form einer Wasserspiegel-Querschnitt-Abfluss Kennlinie benutzt werden.

Literaturangaben

{{#hierarchy-bottom:}}