Wave:AnnualRecurrenceProbability: Difference between revisions
Jump to navigation
Jump to search
m (Froehlich moved page Wave:AnnualRecurrenceProbabilty to Wave:AnnualRecurrenceProbability: typo) |
(add reference) |
||
| Line 2: | Line 2: | ||
[[File:Wave AnnualRecurrenceProbability.png|thumb|right]] | [[File:Wave AnnualRecurrenceProbability.png|thumb|right]] | ||
This analysis method calculates | This analysis method calculates the annual recurrence probility and the return period of annual maxima using the {{:Literature:Weibull_1939|Weibull}} [https://glossary.ametsoc.org/wiki/Plotting_position plotting position] method. | ||
First, the maximum value in each hydrological year is determined. The probability of recurrence and the return period are then calculated using the following formulas: | First, the maximum value in each hydrological year is determined. The probability of recurrence and the return period are then calculated using the following formulas: | ||
| Line 22: | Line 22: | ||
==Notes== | ==Notes== | ||
* If two or more events have the same maximum value, they are assigned the same rank and thus have the same recurrence probability | * If two or more events have the same maximum value, they are assigned the same rank and thus have the same recurrence probability | ||
==Literature== | |||
<references/> | |||
[[Category:BlueM.Wave|A]] | [[Category:BlueM.Wave|A]] | ||
[[Category:Analysis functions|A]] | [[Category:Analysis functions|A]] | ||
Latest revision as of 06:35, 9 December 2023
 Wave | Download | Development
Wave | Download | Development
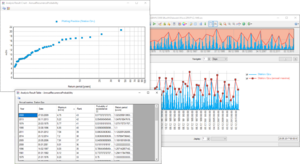
This analysis method calculates the annual recurrence probility and the return period of annual maxima using the Weibull[1] plotting position method.
First, the maximum value in each hydrological year is determined. The probability of recurrence and the return period are then calculated using the following formulas:
[math]\displaystyle{ P = \frac{m}{n+1} }[/math]
and
[math]\displaystyle{ T = \frac{1}{P} }[/math]
where
m: ordered rank of the event (1 = largest event)n: number of total events/yearsP: probability of exceedance [-]T: return period [years]
The analysis results are a result table with all events and their properties, a result chart plotting the return periods and a result series in the main chart containing only the annual maxima.
Notes
- If two or more events have the same maximum value, they are assigned the same rank and thus have the same recurrence probability
Literature
- ↑ Weibull. W. (1939): A statistical theory of strength of materials. Ingeniorsvetenskapsakademiens Handlingar, 151, 1–45