BlueM.MPC theory: Difference between revisions
(Text hinzugefuegt) |
|||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
{{BlueM.MPC nav}} | {{BlueM.MPC nav}} | ||
==Model Predictive Control (MPC) | ==Model Predictive Control (MPC)== | ||
Model predictive control is a method that was first used for process control of chemical plants and oil refineries. MPC is conceptually a method for generating feedback control actions by continuously solving an open-loop optimal control problem over a finite control horizon. MPC systems are characterized by three principles: | Model predictive control is a method that was first used for process control of chemical plants and oil refineries. MPC is conceptually a method for generating feedback control actions by continuously solving an open-loop optimal control problem over a finite control horizon. MPC systems are characterized by three principles: | ||
| Line 12: | Line 12: | ||
For the operation of urban drainage systems only view MPC systems are in operation. Off-line control systems are much more popular. The best known MPC system is the control system of the Quebec Urban Community (QUC) in Canada which is operation since 1999 ({{:Literatur:Pleau-et-al_2005}}). MPC applications of sewer networks are so far not popular since the control constraints (i.e. the available time to calculate control decisions) place restrictions on the degree of sophistication of the process model and the optimization algorithm. In many other technical disciplines MPC is based on linear models. But flow processes in sewer network are highly nonlinear and the proper mathematical description of these processes is based on hyperbolic differential equations. The application of simplified flow routing models is possible but the ability to simulate flows correctly has to be questioned. Further information on MPC applications for urban drainage systems is given in {{:Literatur:Rauch-Harremoes_1999}} and {{:Literatur:Pirsing-et-al_2006}}. | For the operation of urban drainage systems only view MPC systems are in operation. Off-line control systems are much more popular. The best known MPC system is the control system of the Quebec Urban Community (QUC) in Canada which is operation since 1999 ({{:Literatur:Pleau-et-al_2005}}). MPC applications of sewer networks are so far not popular since the control constraints (i.e. the available time to calculate control decisions) place restrictions on the degree of sophistication of the process model and the optimization algorithm. In many other technical disciplines MPC is based on linear models. But flow processes in sewer network are highly nonlinear and the proper mathematical description of these processes is based on hyperbolic differential equations. The application of simplified flow routing models is possible but the ability to simulate flows correctly has to be questioned. Further information on MPC applications for urban drainage systems is given in {{:Literatur:Rauch-Harremoes_1999}} and {{:Literatur:Pirsing-et-al_2006}}. | ||
==Time horizons== | ==Time horizons== | ||
Revision as of 03:25, 20 December 2010
Model Predictive Control (MPC)
Model predictive control is a method that was first used for process control of chemical plants and oil refineries. MPC is conceptually a method for generating feedback control actions by continuously solving an open-loop optimal control problem over a finite control horizon. MPC systems are characterized by three principles:
1. Implementation of a receding horizon strategy.
2. Explicit use of a process model to predict future state developments of the system.
3. Application of optimization algorithms to calculate optimal control settings.
For the operation of urban drainage systems only view MPC systems are in operation. Off-line control systems are much more popular. The best known MPC system is the control system of the Quebec Urban Community (QUC) in Canada which is operation since 1999 (Pleau et al. (2005)[1]). MPC applications of sewer networks are so far not popular since the control constraints (i.e. the available time to calculate control decisions) place restrictions on the degree of sophistication of the process model and the optimization algorithm. In many other technical disciplines MPC is based on linear models. But flow processes in sewer network are highly nonlinear and the proper mathematical description of these processes is based on hyperbolic differential equations. The application of simplified flow routing models is possible but the ability to simulate flows correctly has to be questioned. Further information on MPC applications for urban drainage systems is given in Rauch & Harremoes (1999)[2] and Pirsing et al. (2006)[3].
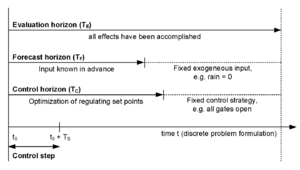
Time horizons
Different time horizons have to be considered in MPC simulations:
- Evaluation horizon: The evaluation horizon is the time span required to evaluate the objective function and therefore equals the simulation period of a single simulation run of the process model.
- Forecast horizon: The forecast horizon is the time span for which inflow boundary values can be computed. Inflow forecast is generally affected with uncertainties, whereas the degree of uncertainty depends usually on the forecast computation method. Rainfall-runoff models are a standard approach to compute inflows from the forecasted rain and can be improved by the evaluation of radar information. Since the forecast horizon might be shorter than the prediction horizon, the inflow boundary values for the remaining time span are estimated.
- Control horizon: The control horizon is the time span for which control decisions for the actuators have to be computed with the optimization algorithm. If the control horizon is shorter than the prediction horizon, the control decisions in the remaining time span have to be extrapolated.
- Control step: The control step is the sampling time during which all control settings have to be found by the optimization algorithm. After finding the optimal settings and delivering this information to the sewer system, the control horizon moves on by the length of the control step and the optimization process is initialized again with the latest sensor information. It is therefore essentially the time step of the control loop.
Literature
- ↑ Pleau, M., Colas, H., Lavallee, P., Pelletier, G., and Bonin, R. (2005): Global optimal real-time control of the Quebec urban drainage system. Environmental Modelling & Software, 20(2005), 401-413,
- ↑ Rauch, W., Harremoes, P. (1999): Genetic algorithms in real time control applied to minimize transient pollution from urban wastewater systems. Water Research, 33(5), 1265-1277, 1999.
- ↑ Pirsing, A., Rosen, R., Obst, B., Montrone, F. (2006): Einsatz mathematischer Optimierungsverfahren bei der Abflusssteuerung in Kanalnetzen. GWF (Wasser - Abwasser), 147(5), 376-383, 2006.