Rural Catchments

{{#hierarchy-top:}}

Die Simulation natürlicher Einzugsgebiete verlangt die Bestimmung der Belastungsbildung, Belastungsaufteilung (oder auch Abflussbildung) und der Abflusskonzentration. Im Folgenden sind die zugrunde liegenden Berechnungsansätze aufgeführt.

Belastungsbildung

Die Belastungsbildung beschreibt die Ermittlung des Gebietsniederschlags für das betrachtete Einzugsgebiet. Pro Einzugsgebiet wird nur ein Niederschlag benutzt. Liegen mehrere Niederschlagsstationen im Einzugsgebiet vor, so ist es zweckmäßig das Gebiet in mehrere Systemelemente 'Einzugsgebiet' zu unterteilen, bis jedem Element wieder nur ein Niederschlag zugeordnet werden kann.

Abflussbildung befestigter / unbefestigter Flächen

Die Abflussbildung ermittelt aus dem gefallenen Niederschlag den Effektivniederschlag und daraus abgeleitet die Komponenten Oberflächenabfluss, Infiltration, Verdunstung und Interflow. Eine Schneeberechnung wird durchgeführt bei Temperaturen unter Null °C und erfolgt anhand des Snow-Compaction-Verfahrens nach Knauf.

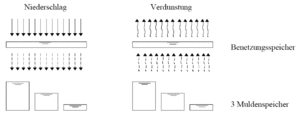
Der natürlich ablaufende Prozess vom Niederschlag zum Abfluss wird für die mathematische Simulation in einzelne Phasen untergliedert. In der Abflussbildungsphase wird die Aufteilung des Niederschlages (Systembelastung) in den direkt zum Abfluss gelangenden "wirksamen Niederschlag" und die abflussunwirksamen Verluste (Benetzungs-, Mulden-, Verdunstungs-und Versickerungsverlust) vorgenommen. Dementsprechend wird diese Phase auch mit Belastungsaufteilung bezeichnet. Die resultierende mathematische Gleichung für die momentane Belastungsaufteilung schreibt sich wie folgt:

[math]\displaystyle{ Nw(t) = N(t) - VP(t) - I(t) - \frac{dO}{dt} - \frac{dS}{dt} }[/math]

mit:

NW = abflusswirksamer Niederschlag

N = Niederschlag

VP = potentielle Verdunstung

I = Infiltration in den Bodenraum

O = Oberflächenwasservorrat

S = Schneevorrat

Nachfolgend werden die in der Gleichung verwendeten Terme und deren Berechnung im Einzelnen erläutert.

Niederschlag N(t)

Die Niederschlagsdaten müssen dem Simulationsmodell in Form von Regenreihen zur Verfügung gestellt werden. Hierbei ist es prinzipiell unerheblich, ob die Niederschlagsreihe ein Blockregen, ein Modellregen, ein gemessener natürlicher Regen, ein Regenspektrum oder eine langjährige Regenreihe ist. Je nach Zielsetzung der Simulationsrechnung ist die geeignete Belastung ausgewählt werden. Die Regenreihen stammen entweder aus der Zeitreihenverwaltung von BlueM oder werden wie bei Anwendung einer Kurzfristprognose durch die Eingabe einer Regendauer, einer Niederschlagshöhe und der Wahl eines Modellregens direkt vor einer Simulation erzeugt.

Verdunstung VP(t)

a) Jahresverdunstungssumme

Abbildung 33: Jahresgang der potentiellen Verdunstung nach BRANDT, 1979

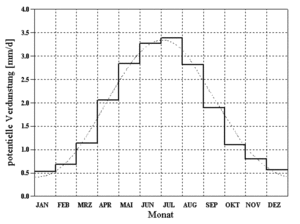
Es wird ein normierter Jahresgang der potentiellen Verdunstung nach Brandt für die Berechnung der potentiellen Verdunstung herangezogen. Aus ausgewerteten Messungen von 20 Stationen, deren Mittelwerte als Histogramm in dargestellt sind, wurde folgende Ausgleichsfunktion (gepunktete Linie in Abbildung 33) ermittelt (BRANDT, 1979). Die potentielle Verdunstung nach Brandt bezieht sich auf die Grasreferenzverdunstung Literature:DVWK???? und geht von einer Jahresverdunstungshöeh von 654,282 mm aus.

[math]\displaystyle{ VP[\mbox{mm/d}] = \begin{cases}(0.96 + 0.0033 \cdot i) \cdot \sin(\frac{2 \pi}{365})(i - 148) + 1.58 & i \lt = 300 \\ 2.56 - 1.53 / 65. \cdot (i - 300.) & i \gt 300 \end{cases} }[/math]

mit

i = laufender Tag des hydrologischen Jahres

i = 1 → 1. November

Wird in der EZG-Datei eine von 654,282 mm abweichende Jahresverdunstungshöhe angegeben, wird der nach Brandt ermittelte Wert entsprechend skaliert.

Abbildung 34: Tagesgang der potentiellen Verdunstung als Vielfaches der mittleren Tagesverdunstung

Ist das gewählte Berechnungszeitintervall kleiner als ein Tag, wird mittels dem in Abbildung 34 dargestellten Tagesgang letztendlich die potentielle Verdunstung für jedes Berechnungszeitintervall ermittelt. Ist das Berechnungsintervall ≥ 1 Tag entfällt die Berücksichtigung des Tagesganges.

b) Verdunstungszeitreihe

Ist eine Verdunstungszeitreihe gegeben (es können nur Tageswerte in der Zeitreihe angegeben werden!), wird der entsprechende Wert des Zeitschrittes eingelesen. Bei einem Simulationszeitschritt < 1d wird der Zeitreihenwert mit dem unter a) erwähnten Tagesgang überprägt.

Oberflächenwasservorrat (Versiegelter Flächenanteil) O

Bei den versiegelten Flächenanteilen kann neben dem Schneevorrat auch die Infiltration vernachlässigt werden, so dass sich die Bilanzgleichung wie folgt vereinfacht:

[math]\displaystyle{ Nw(t) = N(t) - VP(t) - \frac{dO}{dt} }[/math]

wobei die Oberflächenwasservorratsänderung dO/dt die Benetzung der Oberfläche sowie die Auffüllung und Entleerung (durch Verdunstung) der Mulden repräsentiert.

Als Benetzungsverlust BV für versiegelte Flächen wird folgender Standardwert angesetzt.

BV = 0.5 mm

Der Muldenverlust MV wird durch den Anwender vorgegeben. Der Standard- und gleichzeitig Maximalwert im Modell beträgt 1 mm.

Der Muldenverlust stellt den Mittelwert für eine geneigte Oberfläche dar. Da die Mulden jedoch nicht gleichmäßig verteilt sind und erfahrungsgemäß bereits ein Abfluss einsetzt, bevor überall die komplette Muldenauffüllung erreicht ist, wird unterstellt, dass jeweils

Abbildung 35: Schema der Modellansätze Benetzungs- und Muldenverluste

• 1/3 der versiegelten Fläche einen verminderten Muldenverlust von 1/3 MV
• 1/3 der versiegelten Fläche den mittleren Muldenverlust von 3/3 MV
• 1/3 der versiegelten Fläche einen erhöhten Muldenverlust von 5/3 MV

aufweist. Somit kommt es bereits zum Abfluss, wenn der um die Verdunstungsrate verminderte Niederschlag den Benetzungsverlust und 1/3 des Muldenverlustes übersteigt (bei trockener Vorgeschichte). In Abbildung 35 sind die o.g. Annahmen schematisch skizziert.

Der Abflussbeiwert der versiegelten Flächen (nach Abdeckung der Anfangsverluste) wird mit ψ = 1 angesetzt. Bei der Festlegung des versiegelten Flächenanteils in einem Teileinzugsgebiet ist zu beachten, dass nicht alle befestigten oder versiegelten Flächen tatsächlich in eine Kanalisation entwässern.

Die kontinuierliche Bereitstellung der Benetzungs- und Muldenverluste erfolgt über die laufende Bilanzierung dieser Speicher und der Verdunstung.

Oberflächenwasservorrat (unversiegelter Flächenanteil) O

Der Oberflächenwasservorrat wird über die Bilanzierung eines Verlustspeichers in Abhängigkeit des gewählten Abflussbildungsansatzes berechnet. Einzelheiten dazu finden sich in den folgenden Abschnitten zur Berechnung der Infiltration bzw. abflusswirksamer Niederschlag.

Infiltration bzw. abflusswirksamer Niederschlag I(t), Nw(t)

Bei den durchlässigen Flächen kann die Infiltration in den Boden nicht vernachlässigt werden, da diese das Abflussgeschehen entscheidend prägt. Für die Berechnung wurden drei Ansätze im Modell implementiert:

1. Konstanter Abflussbeiwert ψ
2. Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)
3. Bodenfeuchtesimulation

Konstanter Abflussbeiwert ψ

Bei Angabe eines ψ_u-Wertes kommt nach Abdeckung der Anfangsverluste (Benetzungs- und Muldenverlust) der übrige Anteil des Niederschlages im Verhältnis des Abflussbeiwertes ψ_u zum Abfluss und zwar unabhängig von der Vorgeschichte und den Merkmalen des Niederschlages (Höhe, Intensität, Dauer). Auf diesen Ansatz sollte nach Möglichkeit verzichtet werden, da hier der Prozess der Abflussbildung nur grob vereinfachend beschrieben wird.

Ereignisspezifischer Abflussbeiwert in Anlehnung an das Verfahren des Soil-Conservation-Service (SCS)

Bei Angabe eines vom Bodentyp und der Bodennutzung abhängigen CN-Wertes (siehe DVWK, 1991) lässt sich ein vorgeschichtsabhängiger Anfangsverlust sowie eine vorgeschichtsabhängige Beziehung des Abflussbeiwertes von der bis zum betrachteten Zeitpunkt akkumulierten Niederschlagshöhe formulieren (Zaiss, 1987); d.h. der Abflussbeiwert wächst mit zunehmendem Niederschlag im Verlauf des Ereignisses an.

Die Quantifizierung der Vorgeschichte erfolgt über den 21-Tage-Vorregenindex VN

[math]\displaystyle{ V_N = \sum_{j=1}^{21} C(j)^j \cdot h_{N,j} }[/math]

mit

hN,j = Niederschlagshöhe des j-ten Vortags

C(j) = Faktor, der den Einfluss des j-ten Vortags beschreibt

Der Einfluss der Jahreszeit wird durch einen Jahresgang des Faktors C wiedergegeben.

[math]\displaystyle{ C = 0.05 \cdot \sin\left(\frac{2 \pi}{365}\right) (i + 0.75 ) + 0.85 }[/math]

mit

i = lfd. Tag des Abflussjahres

Abbildung 36: Abhängigkeit des Abflussbeiwertes von der Vorgeschichte

Damit schwankt der Wert C zwischen 0,8 < C < 0,9. Hierdurch wird erreicht, dass bei gleichem Vorregen zu unterschiedlichen Jahreszeiten unterschiedliche Vorregenindizes berechnet und damit eine veränderte Abflussbereitschaft in Rechnung gestellt wird.

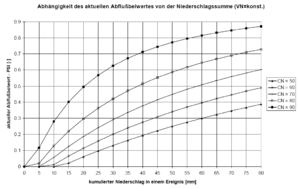
In Abhängigkeit von der auf diese Weise quantifizierten Vorgeschichte kann unter Verwendung der gebietsspezifischen und für mittlere Vorfeuchteverhältnisse gültigen CN-Werte ein aktueller Abflussbeiwert berechnet werden. In Abbildung 36 ist für unterschiedliche CN-Werte dargestellt, wie sich der aktuelle Abflussbeiwert in Abhängigkeit von der Vorgeschichte verändert.

Abbildung 37: Abhängigkeit des Abflussbeiwertes von der kumulierten Niederschlagssumme

Da sich im Verlaufe eines Regenereignisses durch die Durchfeuchtung des Bodens die Abflussbereitschaft eines Einzugsgebiets verändert, wird ebenfalls eine Anpassung des Abflussbeiwertes während eines Ereignisses als Funktion der kumulierten Niederschlagshöhe vorgenommen. In Abbildung 37 ist dieser Zusammenhang für unterschiedliche CN-Werte dargestellt.

Bei der Abhängigkeit der Abflussbereitschaft zum kumulierten Niederschlag bietet TALSIM 2.2 zwei Möglichkeiten:

1. Variabler Verlustansatz (default):
   Die Anpassung eines Verlustwertes für die Funktion des Abflussbeiwertes zum kumulierten Niederschlag erfolgt für jeden Zeitschritt neu.
   (liefert insgesamt höhere Abflussbeiwerte, so dass auf die Berücksichtigung eines Vorregens verzichtet werden kann)
2. Konstanter Verlustansatz:
   Die Anpassung des Verlustwertes erfolgt nur zu Ereignisbeginn einmalig.
   (der Ansatz eines Vorregens ist in diesem Fall zweckmäßig)

Welcher Ansatz bessere Ergebnisse liefert geht nur aus einem Vergleich mit gemessenen Ganglinien hervor. Grundsätzlich ergeben sich mit dem variablen Verlustansatz höhere Abflussspitzen und Füllen bei gleichen Bedingungen.

Eine weitere Möglichkeit zur Beeinflussung der Abflussbildung besteht in der Option, einen Endabflussbeiwert festzulegen. Damit beschränkt man unabhängig vom gewählten Verlustansatz den maximalen Abflussbeiwert. Standardmäßig setzt TALSIM den Endabflussbeiwert auf 1.

Abflusskonzentration

Abbildung 44: Berechnung der Abflusskonzentration von Einzugsgebieten

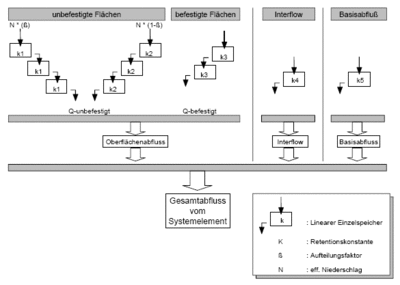
Die Abflusskonzentration bestimmt die Verzögerung des Oberflächenabflusses aus dem Einzugsgebiet. Es wird eine Parallelspeicherkaskade mit drei Speichern für unbefestigte und eine Kaskade für befestigte Flächen benutzt.

Die Speicherkaskaden können entweder als Einzellinearspeicher, oder als nichtlineare Speicher berechnet werden.

Der Abfluss der Komponenten Interflow und Grundwasser wird über einen linearen Einzelspeicher verzögert an den Elementausgang abgegeben (nur bei Bodenfeuchteberechnung!).

Literaturangaben

{{#hierarchy-bottom:}}